定量评价法是较为科学的评价方法，但其计算工作复杂，一般需借助计算机等技术的帮助。该评价方法的关键在于将信息分析成果质量指标数量化，根据各个指标权值的不同，采用小数制、十分制、百分制等计分方式，并结合各种公式进行评分统计，计算出评价结果。目前，在信息分析成果评价过程中主要使用的定量评价方法有：模糊评估方法、综合评分法、科学计量法、经济计量法、蒙特卡洛模拟法等。以下重点介绍模糊综合评价法的应用。

4.4.2.1　模糊综合评价法的概述

模糊综合评价法（Fuzzy Comprehensive Evaluation，FCE）是指借助于模糊数学中模糊变换和综合评判方法对信息分析成果进行模糊综合评价的方法，它应用模糊关系合成原理，从多个因素对被评价事物隶属等级状况进行综合性评价，适用于有模糊概念而又可以量化的场合。科学的评价是以客观性、精确性为基础的，但在实际的评价过程中，所获信息往往是“模糊的”。^[20]

信息分析成果评价的两个重要标准，一是信息分析成果本身的质量，二是评价者的着眼点。构成信息分析成果本身质量的因素很多，评价者的着眼点也有所不同，往往造成评价上的差异。这主要是由于构成评判的指标具有模糊性，这些模糊性指标构成模糊评价集。用模糊评价集表示每个因素的不同等级，并给每个因素赋予不同的权数。这种同时考虑多个因素及各因素的重要程度的评价就是模糊综合评价法，此方法广泛用于管理学领域的各种评价问题。^[21]

模糊综合评价是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法，其特点是评价结果不是绝对的肯定或否定，而是以一个模糊集合来表示。^[22]模糊综合评价法的关键是模糊综合评价模型的建立。

4.4.2.2　模糊综合评价法的基本步骤

（1）建立评价因素集

因素集是以影响评价对象的各种因素为元素组成的一个普通集合，用大写字母U表示，即：

其中，各元素通常都具有不同程度的模糊性，元素ui为第i（i＝1，2，…，n）个评价指标，n为同一层次上评价指标的个数。

（2）建立评语集

评语集是评价者对被评价对象可能做出的各种总的评价结果组成的评语等级的集合。

其中，元素vj为第j（j＝1，2，…，m）种评语，m为评语的种数。

（3）建立成果评价矩阵

利用模糊矩阵和权重集之间的合成运算，得到综合评价结果向量：

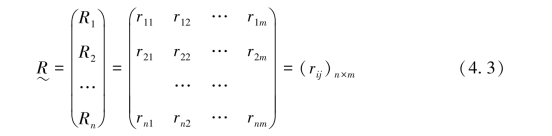
其中，为n×m阶评价矩阵，即从U到V的一个模糊关系。它包含了按评价集V分别对n个评价指标进行评价产生的全部量化信息，Ri＝{ri1，ri2，…，rim}为第i个评价指标的单指标评价，rij为从第i个评价指标着眼对成果所作的第j种评语的可能程度（一般取评语Vj的百分比）。

（4）计算评价指标的权重

各评价指标的权重集合为：

其中，为U上的模糊子集，它所对应的权重向量可用矩阵表示为＝（W1 W2…Wn）；元素Wi为第i个评价指标ui所对应的权重，且满足：

（5）模糊综合评价模型的建立

依据模糊数学的有关理论，成果单层次评价指标的模糊综合评价的数学模型为：

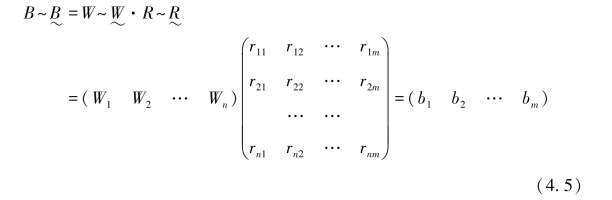
矩阵中的各元素bj就是成果单层次评价指标的模糊综合评价结果。该结果是由模糊矩阵进行乘法运算而得的。乘法运算的步骤与普通矩阵乘法运算的步骤类似，不同之处在于它并非两项相乘后相加，而是先取小后取大。

上述结果通常要进行归一化处理。设处理后的结果为

其中，矩阵中的各元素是经过归一化处理的成果单层次评价指标的模糊综合评价结果，且满足：

在具体实践中，成果评价指标体系往往是多层次的。因此，在单层次模糊综合评价的基础上还应当进行多层次的模糊综合评价。其具体操作因层次多寡而异。总的做法是：在单层次模糊综合评价的基础上，自下而上（即从低层次向高层次）把每层的评价结果作为上一层的输入，逐层计算，直至最后得出总的模糊综合评价结果。

此外，上述结果仅仅是针对某一成果进行模糊综合评价的结果。为了进行一批成果的比较和选优，人们常将其结果用一个总分值来直观地表示。总的做法是：首先将评语集V的各元素取以相应的量化值，然后将每个评价结果乘以相应的分值，并求总分S，即：

比如，如果采用9分制对5种评语评分，则可将量化分值做出如表4.8的规定。由此，我们可以计算出某一成果模糊综合评价结果的总分为：

表4.8　评语的分值

(www.daowen.com)

模糊综合评价法应用案例

模糊综合评价法在高校科研项目绩效评价中的应用^[23]

科研项目的绩效评价是政府科学管理的重要手段之一，也是高校进行科研项目管理的核心内容。对高校的科研项目进行科学、高效和合理的评估，不仅可以适应新时代的科研发展要求，以科学的理论指导高校科研的发展，而且能够纠正部分高校在科研项目管理方面的偏差与不足，减少决策失误，使有限的科研项目资金发挥最大的效益。但是在实际评估的过程中，绩效评价会涉及评级问题，而评级是人们在以往认识基础上的主观判断，不可避免地使绩效评价带有一些认识上和结论上的模糊性。因此，需要一种科学的评价方法来避免人为的主观判断造成的偏差，以此来提高绩效评价的客观性和有效性。模糊综合评价法正是基于这种情况提出的，它建立在严谨、科学的数学原理基础上，能够为高校科研项目绩效评价提供实际有效的依据。

一、解析模糊综合评价法

第一步，建立模糊评判矩阵。首先，对某个因素进行评价，设该因素的指标集合为U＝{U1，U2，…，Un}，该因素的评价集合为V＝{V1，V2，…，Vm}，每个评价Vk（k＝1，2，…，m）表示对每个因素作出的评价等级，那么对每一个因素的模糊评价就是评语集合上的一个模糊子集。其次，设第i个因素的模糊评价为Ri＝{ri1，ri2，…，rim}（i＝1，2，…，n），其中rik表示第i个因素的第k个评语。最后，如果有n个模糊评价向量（R1，R2，…，Rn），则构成了因素指标集合到因素评价集合的模糊关系，此时，模糊评判矩阵可以表示为：

第二步，对每个单因素进行模糊分析。得出模糊评判矩阵后，可以在因素指标集合上取它的一个子集Ui，然后对这个子集给定一个模糊向量Ai＝（ai1，ai2，…，ain），来表示它，这个向量的每一个值为aik（k＝1，2，…，m），则表示这个因素在模糊评价中的重要性，可以定为权重Wik第一步中已经给定了模糊评价向量Ri，结合本步骤给出的模糊向量Ai，可以得出某个因素的评价向量为Bi＝Ai×Ri＝（bi1，bi2，…，bim）（i＝1，2，…，k）。

第三步，对此因素进行模糊综合评价。假设模糊权重向量为A＝（a1，a2，…，ak），模糊评价矩阵为R＝（B1，B2，…，Bk）T＝（bij）k×m，可以得出模糊综合评价向量为B＝A×R＝（b1，b2，…，bm）。

第四步，得出模糊评价值P。对因素的评价集的每个评价结果给定一个固定分值区间，假设评价集为H＝（h1，h2，…，hm），则最后得到的模糊评价分值为P＝B×HT。对应不同分值区间划分出的几个评价等级，就得到所评价因素所属的等级水平。

二、模糊综合评价法在实际案例中的应用

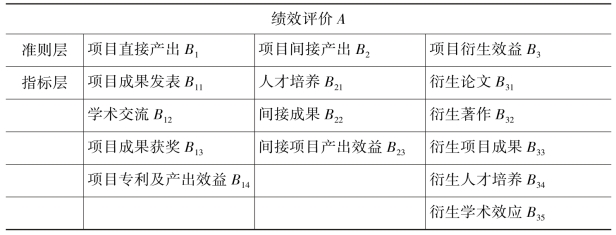
以河南省某高校的科研项目管理为例，具体说明模糊综合评价法在高校科研项目绩效评价中的应用。针对目前河南省高校科研项目的绩效考评实际情况，将指标体系分为两个层次，即准则层和指标层。其中准则层包括项目直接产出B1、项目间接产出B2和项目衍生效益B3三大类。这三大类再具体分类为表4.9的指标层。

表4.9　河南省某高校科研项目绩效评价指标体系

综合应用层次分析法和专家评判法，计算准则层的权重值如表4.10所示。

表4.10　准则层权重值

综合应用层次分析法和专家评判法，计算指标层的权重值如表4.11、表4.12和表4.13所示。

表4.11　项目直接产出B1指标权重值

表4.12　项目间接产出B2指标权重值

表4.13　项目衍生效益B3指标权重值

根据表4.9确定评价因素的指标集合为A＝{B1，B2，B3}，其中准则层的B1，B2，B3分别表示河南省某高校科研项目的项目直接产出、项目间接产出和项目衍生效益。指标层Bi＝{Bij}（i，j＝1，2，3）为河南省某高校科研项目绩效评价过程中的评价指标的子集。

依据前面建立模糊评判矩阵的步骤，确定河南省某高校科研项目绩效评价的评价等级及其对应标准。假设绩效评价集为V＝{V1，V2，V3，V4，V5}，相对应的评价等级表示为{十分优秀，比较好，基本达标，需要整改，极差}。对上面的5个等级均给定一个分值区间，那么{十分优秀，比较好，基本达标，需要整改，极差}相对应的分值集合为H＝{95，80，65，50，35}。如果规定最终得分在90分以上该校的科研绩效管理评价为十分优秀，那么得分在75～90分的评价就是比较好，60～75分的评价为基本达标，40～60分的评价为需要整改，40分以下则表示该校的绩效管理评价为极差。

由表4.9～表4.13可知，在河南省某高校的科研项目绩效评价中，各评价指标的权重向量表示为：

准则层权重向量WA＝{0.5，0.2，0.3}

指标层权重向量WB1＝{0.45，0.15，0.2，0.2}

WB2＝{0.25,0.4,0.35}

WB3＝{0.3,0.15,0.2,0.2,0.15}

最后，建立河南省某高校科研项目绩效评价的模糊评判矩阵。在实际操作中选定了5位负责河南省高校科研项目管理的专家，他们根据该校科研项目的实际情况，对表4.9指标层的指标分别进行打分。由于每个指标的评价都是具有模糊性的，在方法处理上综合了每位专家对某一个指标的打分次数，用5位专家赞同该相应指标的评语等级的比重作为这个指标对应于某个评价集合的隶属度，得到模糊评判矩阵，计算结果表示如下：

得到某个因素的模糊评价Bi＝WBi×RBj

得到指标的模糊综合评价B＝WA×R＝（0.093，0.491，0.265，0.151，0）T。得出模糊综合评价值P＝B×HT＝72.89分。参考先前设定的评价等级标准，可知该校的绩效评估结果为基本达标。

三、结束语

模糊综合评价法计算精确，操作过程简便，为高校科研项目管理的绩效评估提供了科学依据，但由于各个高校的情况不同，在评价时很难考虑到所有指标和情况。因此，如何更准确地判定高校科研项目管理的优劣及绩效水平，仍需要更有效的数学模型。