表3.13显示了某年度省会城市和计划单列市的主要经济指标，下面通过社会科学统计分析软件SAS做主成分分析，试图得出各城市的综合经济得分并排列名次。

表3.13　某年度省会城市和计划单列市主要经济指标

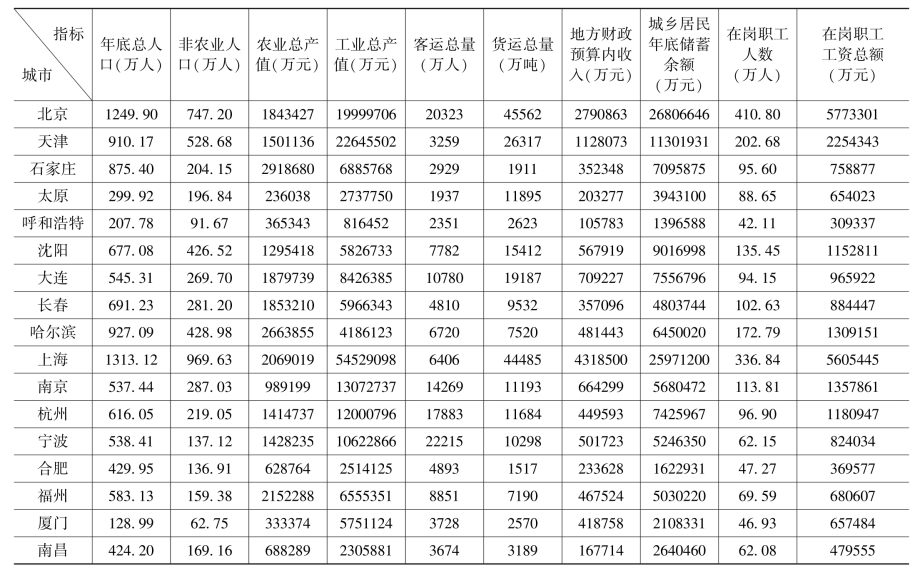
续表

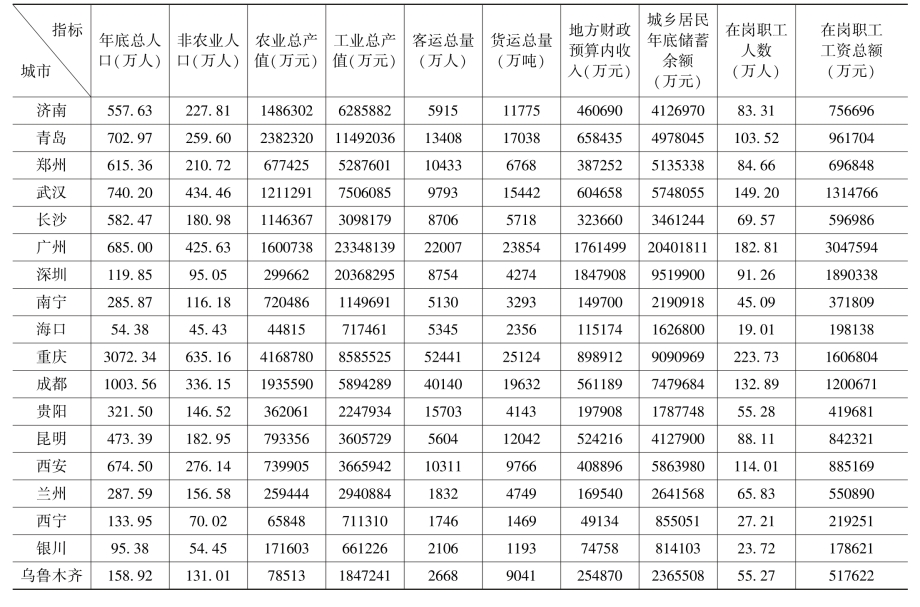
在SAS的主成分分析中，选择的变量为x1（年底总人口）、x2（非农业人口）、x3（农业总产值）、x4（工业总产值）、x5（客运总量）、x6（货运总量）、x7（地方财政预算内收入）、x8（城乡居民年底储蓄余额）、x9（在岗职工人数）、x10（在岗职工工资总额），共10个变量。默认情况下，系统基于原变量的相关矩阵进行主成分分析。

通过SAS进行计算，可得样本相关矩阵，如图3.19所示。

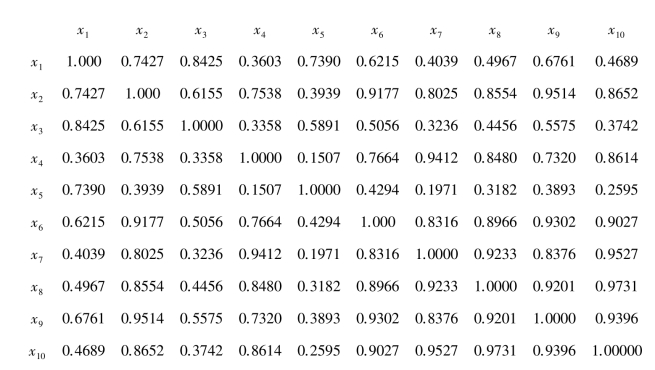
图3.19　样本相关矩阵

以上相关矩阵的特征值、各标准化主成分的贡献率及累计贡献率见表3.14。

表3.14　相关矩阵的特征值及贡献率

续表(www.daowen.com)

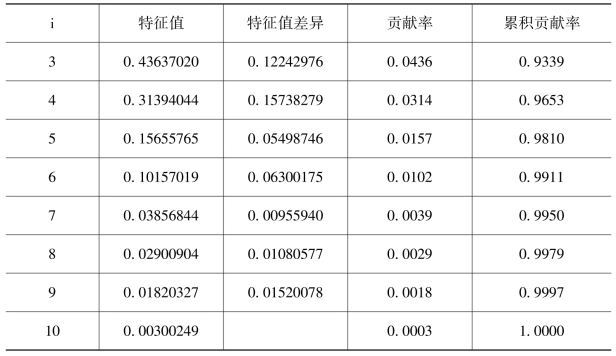
以上相关矩阵的标准化特征向量见表3.15。

从表3.14可知，第一主成分贡献率为71.40%，前两个主成分的累积贡献率为89.03%。表3.14中的xi∗为原变量xi标准化后的新变量，则第一标准化样本主成分为：

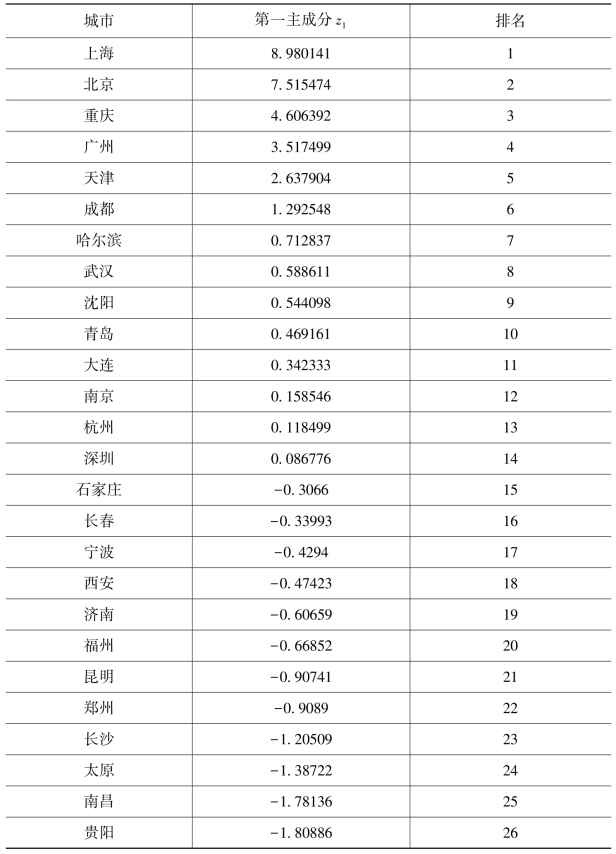
z1近似为10个标准化变量xi∗（i＝1，2，…，10）的等权重之和（x5∗权重稍小一些），是反映各城市经济实力的综合指标，z1的值越大，则该城市的综合经济实力越强，由于z1的贡献率高达71.40%，所以基本上可用z1的得分值对各城市进行排序。通过SAS进行计算，各样本按第一主成分得分及排序见表3.16。

表3.15　标准化特征向量

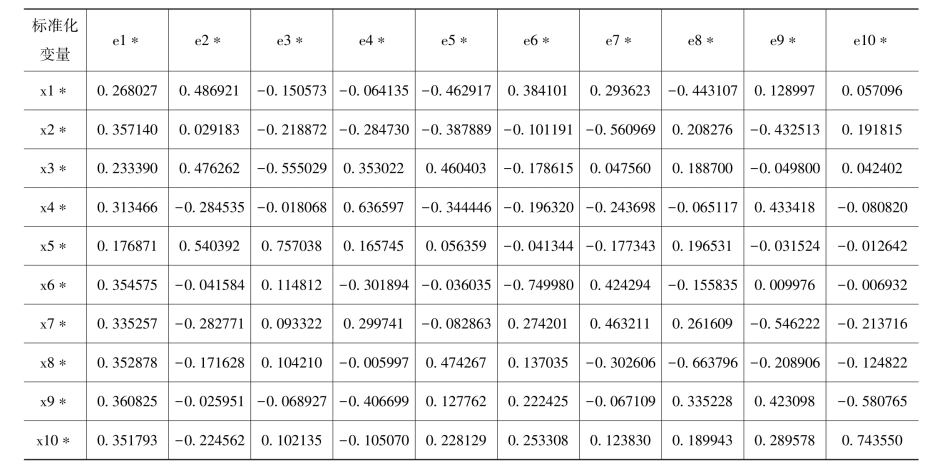
表3.16　按第一主成分得分及排序

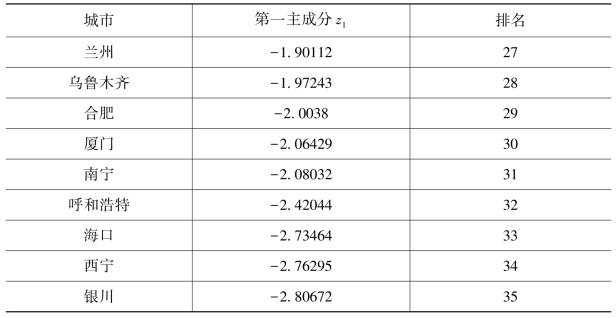
续表

第二个主成分z2的系数表明，它主要反映的是第1、3、5个变量的信息。关于主成分的实际意义，要结合具体问题和相关专业知识给予合理的解释。