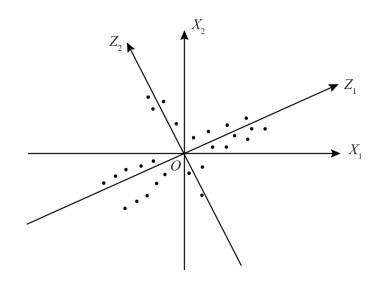
下面以二元变量X＝（X1，X2）为例，说明主成分分析法的思想。对此二维变量进行了n次观测，得数据xi＝（xi1，xi2）（i＝1，2，…，n），假设它们在二维平面X1OX2上的分布如图3.18所示。先考虑如下的一种极端情形，X1和X2的相关系数的绝对值为1，即（xi1，xi2）（i＝1，2，…，n）分布在一条直线l上。若将原坐标系沿逆时针方向旋转一个角度θ得新的直角坐标系Z1OZ2，使坐标轴OZ1与l重合，这时观测点（xi1，xi2）可由它们在OZ1上的坐标所确定，即原来的二元变量所表达的信息等同于转化后一元变量（主成分）所表达的信息。由解析几何可知，这些观测点在OZ1上的坐标为：

它们是原观测数据的线性组合且在OZ1轴上的分散性（即样本方差Var）达到最大。因此，对原变量（X1，X2）作适当的线性变换可得新的变量Z1，即：

其中θ的选择使Var（Z1）最大且Z1的相应值完全可以反映原二元变量（X1，X2）的观测值的分布状况。

一般情况下，将OX1轴沿逆时针方向旋转一个角度θ到OZ1轴，使得原观测数据（xi1，xi2）经过线性组合后所得的新变量Z1具有最大的分散性，即该方向所含的数据间差异的信息最多。相应地，OX2转至OZ2方向。在现实世界中，原变量（X1，X2）是可直接观测的变量，变量（Z1，Z2）是不可直接观察和测量的，它们通过原变量的线性变换而得到。设转过角度为θ，则观测点（xi1，xi2）在新坐标系下的坐标为：

(www.daowen.com)

图3.18　主成分分析示意图

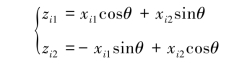
这时，（zi1，zi2）（i＝1，2，…，n）均是相应的原数据的线性变换，且线性变换系数满足条件：sin2θ＋cos2θ＝1。（zi1，zi2）完全反映了原始数据的分布情况，并且各自反映的是彼此不相关的两个方向上的分散性。相应的变量：

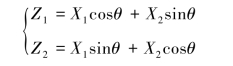
分别称为X1和X2的第一主成分和第二主成分。如果数据在OZ2方向上的分散性很小，那么可用一元数据zi1，i＝1，2，…，n反映原二元数据的绝大部分信息，即可近似地用Z1的分布信息代替原二维变量（X1，X2）的分布信息。