时间序列分解法的基本思想是将时间序列上构成波动的不同因素分离开来，对各因素分别进行分析。这种方法有助于说明各种社会经济活动中的数量指标发生变动的分量原因，既有利于准确预测，又有利于有的放矢地进行控制和管理。

3.4.4.1　时间序列的结构形式

在社会经济活动中，时间序列值依时间波动通常是由于受到下列因素的影响：

（1）趋势（T）因素：当时间序列值依时间变化时，表现出某种倾向（如线性、指数曲线或S形曲线趋势）。它是影响时间序列值的主导因素。

（2）循环（C）因素：它是周期不固定的波动变化（如经济危机）产生的原因。

（3）季节变动（S）因素：它是周期相对固定（如一年四季）的波动变化产生的原因。

（4）不规则变动（I）因素：它是指许多外生的不易控制的因素。这些因素的出现带有很大的随机性。一般假定E（I）＝0，D（I）＝σ2。

若以Yt表示时间序列值，Tt、Ct、St、It分别表示趋势、周期、季节变动和不规则变动，则时间序列值可分解为以下3种模式：

3.4.4.2　时间序列的传统分解

在以上各种模式中，实际常用的是乘法模式。在该模式中，各变量的单位是：Tt与Yt有相同的单位，其他因素的变化均是比例值。为了求出各因素对时间序列值影响的大小，下面介绍一下各因素的分解方法。

（1）分解出Tt与Ct。假定季节长度为4（即一年分为4季）。由假定E（I）＝0可知，只要将序列Yt作移平跨度为4的移动平均，就可消除季节变动和不规则变动的影响。记移动平均值为M，则：

（2）分解出St与It。将式3.41两边除以Mt，得：

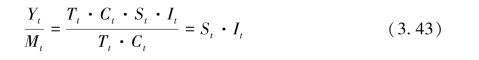
（3）从StIt中分解出St。式3.43中的StIt包含了季节变动因素和不规则变动因素，因此要设法排除掉不规则变动因素。式3.42的移平法虽然可消除不规则变动因素，但同时也消除了季节变动因素。为了消除不规则变动因素而保留季节变动因素，我们采用按季节平均的方法。例如，将式3.43所得的序列StIt逐年逐季排列起来，然后将各年的相同季节的StIt相加进行平均，这就达到了消除不规则变动因素而保留季节变动因素的目的。详见下面的同季平均法。

（4）从TtCt序列中分解出Ct。TtCt包含了趋势因素与周期因素，要把这两者分离出来，先要确定一种能最好地描述数据的趋势变化的曲线类型，曲线的模型建立和参数估计与前面章节中论述的方法相同。由曲线方程估算出Tt，以Tt除Mt，得：

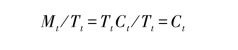
3.4.4.3　常用时间序列分解预测法(www.daowen.com)

利用时间序列分解法进行预测的常用方法主要有同季（月，下同）平均法、季节系数法等。同季平均法是分析具有季节变化的时间序列并在此基础上进行预测的最简单的方法，主要适用于受季节变化影响而无明显趋势变化的时间序列。它包括两个步骤：一是将历年同季数据的平均值与各季总平均值相比，求得季节系数；二是以最近一年的各季平均值分别乘以各季节系数，即得来年各季的预测值。季节系数法是分析具有趋势变化和季节变化的时间序列并在此基础上进行预测的一种方法。该方法通过分析数据的趋势变化和季节波动规律，建立趋势变动模型，求出季节系数，然后再用季节系数去修正反映趋势变化的模型。这种方法的提出主要基于这样一种思想，即趋势是时间序列在整个长时期内的平均运动，是制约时间序列波动的主导因素，而其他各因素引起的波动只能算是对趋势的偏离。

现举一例说明同季平均法的应用。

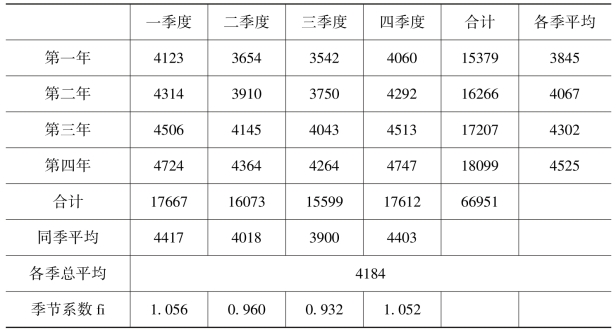
例：试根据表3.12中历年数据预测某商场某电器产品的销售量。

表3.12　某电器销售量（台）和季节系数表

解：

（1）计算同季平均值和各季总平均值。

同季平均值是历年同季数据之和除以总年数；各季总平均值是历年全部季度总销售数除以总的季数。其结果列于表3.12。

（2）计算季节系数。

季节系数fi等于同季平均值与各季总平均值之比：

f1＝4417/4184＝1.056

f2＝4018/4184＝0.960

f3＝3900/4184＝0.932

f4＝4403/4184＝1.052

（3）计算预测值。

以第四年的季平均值分别乘以各季节系数fi，即得第五年各季的预测值：