生长曲线是增长曲线的一大类，是描绘各种社会、自然现象的数量指标依时间变化而呈某种规律性的曲线。由于生长曲线形状大致呈“S”形，故又称“S”曲线。在信息分析中，利用生长曲线模型来描述事物发生、发展和成熟的全过程的方法就是生长曲线法。

生长曲线法是基于对事物发展全过程的认识而发展起来的。事物的发展（如人口的增长、信息量的增长、技术的发展等），开始几乎都是按指数函数的规律增长，在达到一定程度后，由于自身和环境的制约作用，逐渐趋于一种稳定状态。生长曲线较好地描述了事物的这种发生、发展和成熟的全过程。生长曲线有两种，一种是对称型的生长曲线，如图3.17（a），又称逻辑（Logistic）曲线或珀尔（Pearl）曲线；另一种是不对称型的生长曲线，如图3.17（b），又称龚珀兹（Gompertz）曲线。

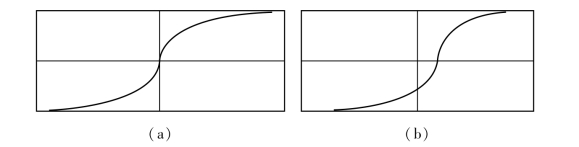
图3.17　生长曲线

3.4.3.1　逻辑曲线

（1）数学模型。

美国统计学家珀尔（Pearl）通过对生物繁殖和生长过程的大量研究，提出了一个模拟生物生长过程的逻辑曲线模型。其数学表达式为：

式3.33中，k＞0，a＞0，b＞0。

这个模型同样适用于人口增长、信息量的增长、技术的发展等过程，因而在信息分析中应用广泛。

逻辑曲线具有以下数学特征：

①当t→∞时，y→k，即k是y值变化的上限。

②将y对t求一阶导数，得：

∴在（－∞，＋∞）上，y′＞0，该曲线单增，无极值。

③将y对t求二阶导数，得：

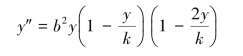
当y＝0，y＝k和时，y″＝0，这表明该曲线在其单增区间内，y＝k 2是唯一拐点，拐点的上下两部分相对于拐点是对称的。

将代入式3.33，得：

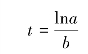
∴该曲线的拐点为。

④通过改变a或b的数值，可以对它的形状和位置独立地进行控制。改变a只影响曲线位置，而不改变其形状；相反，改变b只影响形状而不改变其位置。

（2）模型系数的确定。

确定系数k，a，b的方法有多种，具有代表性的有：

①线性回归法

通过定性分析的方法，根据事物发展规律确定上限k值。

对曲线进行线性化变换：

令

则

根据回归分析法，用最小二乘法求出系数。

②三段和值法

对式3.33两边取倒数，并令

式3.34是修正指数曲线的形式，可通过三段和值法来求系数。

三段和值法解决问题的基本出发点是将整个序列分为三个相等的时间周期。假定有3n组数据（t0，Y0），（t1，Y1），…，（tn－1，Yn－1）；（tn，Yn），（tn＋1，Yn＋1），…，（t2n－1，Y2n－1）；（t2n，Y2n），（t2n＋1，Y2n＋1），…，（t3n－1，Y3n－1），n为任意整数。一般来说，n值越大，估计的精度就越高。

上述3n组数据应分别满足式3.34。若以i代替ti[i＝0，1，…，（3n－1）]，则可得下述三组方程组：

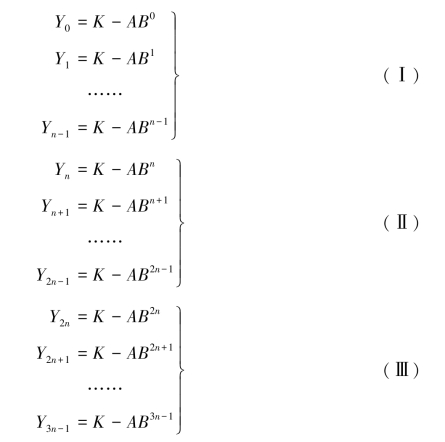
将上述方程组左右两边分别相加，求解得

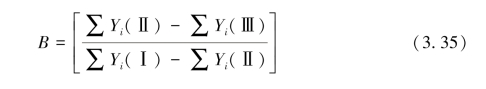
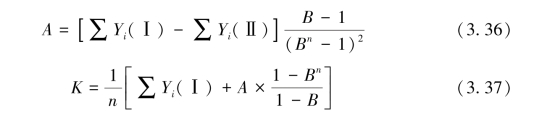
由式3.35、式3.36和式3.37求出B，A，K后，即可得逻辑曲线模型的系数k，a，b。

（3）计算实例。(www.daowen.com)

根据表3.11列出的某种技术参数的时间序列数据预测未来一期参数值。

表3.11　原始时间序列数据及其倒数

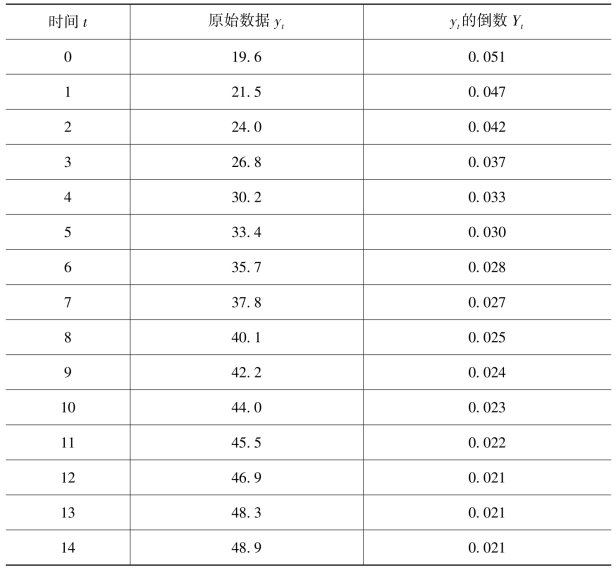
解：先求Yt＝1/yt，并填于表3.11中。

将Yt分为3组：

∴逻辑曲线模型为：

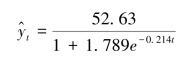
由此得下一期参数预测值为：

3.4.3.2　龚珀兹曲线

（1）数学模型。

英国统计学家和数学家龚珀兹（B.Gompertz）提出了另一个生长曲线模型，即龚珀兹曲线模型。其数学表达式为：

式中，k＞0，0＜a＜1，0＜b＜1。

龚珀兹曲线具有以下数学特征：

①当t→－∞时，y→0；当t→∞时，y→k，即y值在0～k变化，k为上限。

②将y对t求一阶导数，得：

将式3.38两边取自然对数，得：

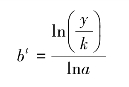
将bt代入式3.39，得：

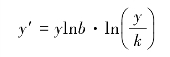
由上式可知，除y＝0和y＝k外，在0～k的一切y值均不能使y′等于0，即该曲线是单调的，无极值。

③将y对t求二阶导数，得：

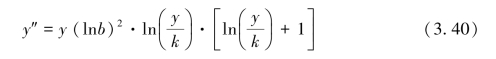
由式3.40可知，除y＝0，y＝k外，只有当时，y″＝0，所以龚珀兹曲线在单调区间内存在唯一的拐点。可以算出该曲线的拐点为：

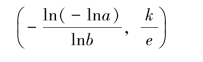
由于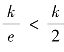，故龚珀兹曲线的拐点位置比逻辑曲线的拐点更低，龚珀兹曲线拐点前后两部分是不对称的。

④t＝0时，y＝ka，即曲线与y轴相交点为（0，ka）。

（2）模型系数的确定。

具有代表性的模型系数确定方法有：

①线性回归法

首先，通过定性分析的方法，根据事物发展规律确定上限k值。

其次，对曲线进行线性化变换，将式3.38变形后两边取自然对数，并令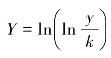，则

最后，根据回归分析法，用最小二乘法求出系数。

②三段和值法

对式3.38两边取常用对数，并令lgy＝Y，lgk＝K，lga＝－A，b＝B，则

具体计算与逻辑曲线模型系数的三段和值求法完全相同。在求出A、B、K后，即可得龚珀兹曲线模型系数a，b，k。