指数平滑(S)法是对移动平均法的改进。我们进一步考察移动平均法,可以看出,在式3.14中,每个数据权重相等,均为1/n,这意味着不同时间上的数据具有相同的价值,这在一般的预测中显然是不合理的。如果认为参加计算的每一数据对预测结果的影响程度不同,就应该对这些数据分别给予不同的权值。指数平滑法正是基于这一思想。权值的选择取决于信息分析人员的预测经验。由于近期数据的影响较大,通常可赋予较大权值。
本节所讨论的指数平滑法实质上是指数加权移动平均法。
3.4.2.1 一次指数平滑
(1)基本公式。
若以α代表权数,则原始时间序列数据的加权移动平均值可表示为:
![]()
其中,α1>α2…>αn
且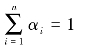
若α1,α2,…,αn呈等比数列,公比为γ=1-α,则权数数列为:
α,α(1-α),α(1-α)2,…![]()
类似地有:
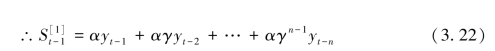
由式3.21和式3.22得
![]()
由于αγnyt-n很小,可忽略不计,于是
![]()
(2)平滑常数α的含义及取值。
①预测结果对α的依赖性
α的取值反映了新旧数据所占的分配比例,对预测结果直接产生影响。因此,预测的结果依赖于α的选择。
α的取值有两种极端情况:
当α=0时,![]() ,即平滑值维持不变;
,即平滑值维持不变;
当α=1时,![]() ,即平滑值等于最新的观察值。
,即平滑值等于最新的观察值。
一般地,α选得小一些,预测值趋向就较平稳,“修匀”效果越显著;α选得大一些,近期数据所占的比重越大,对变化的反映越灵敏,但“修匀”的效果越不明显。
②α值与n值的关系
在对波动曲线的“修匀”作用上,α值与n值的取值方向正好相反。即在移动平均法中,n值越大,“修匀”效果越显著;而在指数平滑法中,α值越小,“修匀”效果越显著,即![]() 。在实际应用中,一般取
。在实际应用中,一般取

③α取值的经验选择
如果我们希望选取的α值使预测误差的方差尽可能小的话,那么α值的选择就应以残差平方和最小为标准,即α值应使:
![]()
这里Q是α的函数,一般可采用0.618法求出使Q达到最小值的α值。
根据一般的经验,α的取值范围通常是0.01≤α<0.3。
(3)计算实例。
根据表3.10中所列的一组时间序列数据yt,分别取加权系数α=0.3和α=0.1,计算其一次指数平滑值。
表3.10 原始数据及一次、二次、三次指数平滑值计算结果
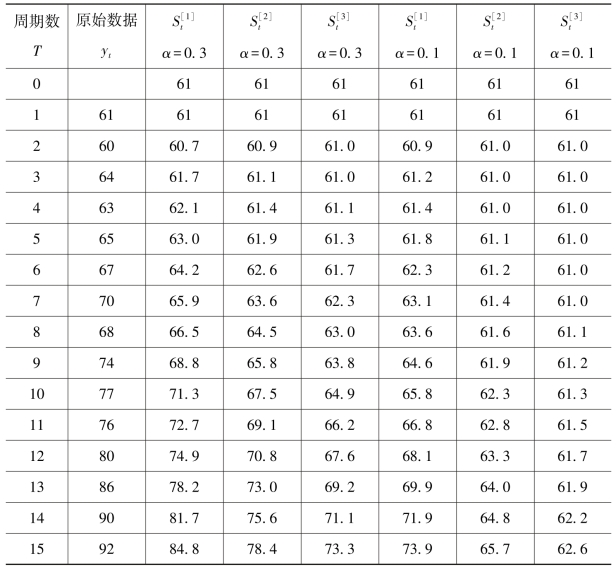
解:先设初始值![]() ,按式3.22计算α=0.3的一次指数平滑值,并填于表3.8中。
,按式3.22计算α=0.3的一次指数平滑值,并填于表3.8中。
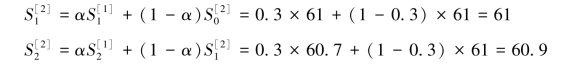
……
以同样方法逐项计算α=0.1时的![]() ,并填于表3.9中。
,并填于表3.9中。
3.4.2.2 二次指数平滑
(1)基本公式。
二次指数平滑是对一次指数平滑值![]() 再进行一次平滑,计算公式如下:
再进行一次平滑,计算公式如下:
![]()
(2)计算实例。(https://www.daowen.com)
根据表3.8中的计算数据![]() ,分别取加权系数α=0.3和α=0.1,计算二次指数平滑值。
,分别取加权系数α=0.3和α=0.1,计算二次指数平滑值。
解:先设初始值![]() ,按式3.25计算α=0.3的二次指数平滑值,并填于表3.8中。
,按式3.25计算α=0.3的二次指数平滑值,并填于表3.8中。
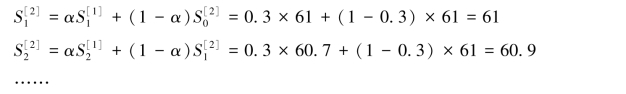
以同样方法逐项计算α=0.1时的![]() ,并填于表3.8中。
,并填于表3.8中。
3.4.2.3 模型与计算
与移动平均法相似,当时间序列数据有线性趋势时,![]() 对yt、
对yt、![]() 对
对![]() 也存在滞后偏差的问题。因此,
也存在滞后偏差的问题。因此,![]() 只能用于简易预测。为了改善预测效果,我们可以利用
只能用于简易预测。为了改善预测效果,我们可以利用![]() 求出平滑系数,建立线性指数平滑模型再进行预测。
求出平滑系数,建立线性指数平滑模型再进行预测。
设已观察到时间t以前的序列值yt,现要预测未来时刻t+T的序列值。由于序列具有线性趋势,因此可假定线性指数平滑模型的一般形式为:
![]()
这里,![]() 为第t+T周期的预测值;T为由目前周期t到需要预测的周期之间的周期个数;at与bt为平滑系数(at为截距,bt为斜率),依赖于t以前的yt观察值。at、bt的计算公式为:
为第t+T周期的预测值;T为由目前周期t到需要预测的周期之间的周期个数;at与bt为平滑系数(at为截距,bt为斜率),依赖于t以前的yt观察值。at、bt的计算公式为:

下面给出一个计算实例。
根据表3.10中的计算数据,建立线性指数平滑模型并计算未来2期的预测值。
解:取α=0.3,由表3.8查得:
![]()
代入式3.27得:
![]()
代入式3.28得:

∴预测模型为:
![]()
以T=1、2分别代入上式得未来2期的预测值:
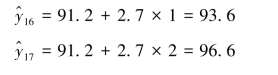
3.4.2.4 三次指数平滑
除了线性指数平滑模型外,还有非线性指数平滑模型。后者一般采用三次指数平滑法,它几乎适用于所有的应用问题,因而使用比较广泛。
(1)基本公式。
![]()
(2)非线性指数平滑模型的建立。
非线性指数平滑模型的一般形式为:
![]()
这三个平滑系数的计算公式如下:
![]()
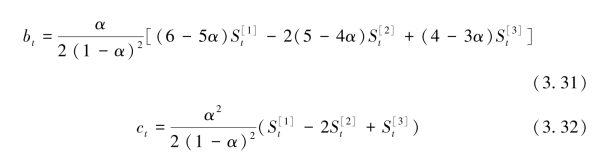
(3)计算实例。
根据表3.10中的计算数据,建立非线性指数平滑模型,并计算未来2期的预测值。
解:
①计算三次指数平滑值。其计算方法与一、二次指数平滑值的计算方法相似,分别取α=0.3,α=0.1,按式3.29计算得结果,并填于表3.10中。
②计算平滑系数并求出平滑模型。取α=0.3,由表3.10查得,![]()
![]()
代入式3.30、式3.31和式3.32可得:
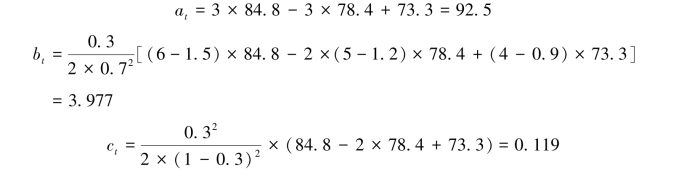
∴预测模型为:
![]()
③计算未来2期的预测值。以T=1、2分别代入上式,得:
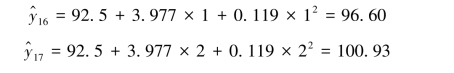
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






