在分层聚类中，样品一旦被归到某个类后就不变了，这要求分类方法比较准确，而这在不清楚各个类的形状之前是比较难以做到的。另外，样品容量较大时，分层聚类法的计算量过大，一般情况下，分层聚类要求样品数量不超过200。在数据分析中，通常数据量越大，分析效果越好，并且数据仓库技术为提供大批量数据打下了基础。因此，分层聚类在样品数量上的限制将日益显示出其不足。为了弥补分层聚类的不足，产生了快速聚类法。快速聚类法已成为生成一组聚类的常用方法之一，几乎任何商业数据挖掘应用程序都在不同程度上集成了这种聚类分析算法。

3.3.4.1　快速聚类法概述

快速聚类法的主要特征是可以根据需要预先确定k个聚类。根据选定的k值，聚类可以产生两个完全极端的结果。如果设k等于1，就可能会得到一个没有意义的结果，因为所有的数据会归类到一个节点中。另一个极端是设k等于样品数，同样也会得到一个毫无意义的结果。任何其他的聚类个数取决于k值，对于k值的选取没有一个固定的规则，常常需要对各种取值进行反复试验。快速聚类如图3.11所示。

图3.11　快速聚类示意图

3.3.4.2　快速聚类法的具体步骤

（1）选择聚点。

聚点（种子）是一批有代表性的样品，它的选择决定了初始分类，对最终分类也有较大影响。当数据对象确定后，算法首先确定可能存在的聚点。选择聚点有多种方法。一是凭经验进行选择。如果对研究对象比较了解，从以往的经验出发，基于某个特征确定k个明显不同的样品作为聚点。二是随机法。将n个样品人为地（或随机地）分成k类，以每类的重心作为聚点。三是最小最大原则。设要将n个样品分成k类，先选择所有样品中相距最远的两个样品xi1、xi2作为前两个聚点，即选择xi1、xi2，使

然后，选择第3个聚点xi3，使得xi3与xi1、xi2的距离最小者等于xi1、xi2以外所有样品与xi1、xi2的距离最小者中的最大者，即

再按相同的原则选取xi4，依次下去，直至选定k个聚点xi1，xi2，…，xik。

一般情况下，若已选了l个聚点（l＜k），则第l＋1个聚点选取的原则为：

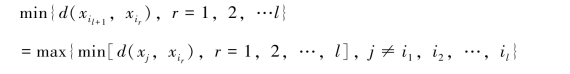
（2）初始分类。

设k个初始聚点的集合是：

用下列原则实施初始分类：

即，初始分类的原则是每个样品以最靠近的初始聚点L（0）归类，最后将所有样品分成不相交的k个初始类：

（3）从G（0）出发，计算新的聚点集合L（1）。

以G（0）的重心作为新的聚点：

其中ni是类中的样品数，这样，得到新的聚点集合：

(www.daowen.com)

从L（1）出发，对样品进行新的分类：

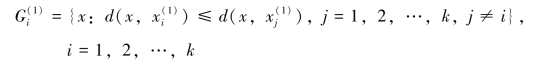
同样，此次分类的原则是每个样品以最靠近的聚点L（1）归类，最后将所有样品分成不相交的k类：

按照这种方法依次迭代计算下去。

（4）设在第m步得到分类。

在以上迭代计算过程中，是类的重心。不一定是样品，通常也不是的重心。当m逐渐增大时，分类趋于稳定。此时，就会近似为的重心，从而算法即可结束。理论上，从某一步m开始，分类与会达到完全相同，计算即告结束。实际计算时，设

给定ε＞0，若d（m）≤εd（0）

则迭代计算过程结束。

实际计算中，可事先确定一个迭代次数，可能在迭代次数内达到，也可能以迭代次数作为计算结束的标志，此时，。

3.3.4.3　快速聚类法应用分析

表3.7是某年度20个代表性地区农村居民家庭平均每人生活消费现金支出情况，下面利用SPSS的快速聚类法对这些地区进行分类。在参数选择中，k选为2。

图3.12是初始聚点，对照表3.7，可以看出，第一个聚点是上海，第二个聚点是甘肃。这两个聚点是所有样品中距离最远的两点。图3.13显示了迭代过程，一共进行了2次迭代。两类的第一次聚点变化分别为369.780和271.320；两类的第二次聚点变化分别为0，聚类即告结束。

图3.14显示了各类的成员，第一类包括北京、上海、浙江和广东，属农村居民家庭平均每人生活消费现金支出较高的地区；第二类包括剩余的地区，属农村居民家庭平均每人生活消费现金支出较低的地区。可见，用快速聚类法将样品分成两类的分类结果与采用最长距离算法的层次聚类的分类结果相同。图3.15是快速聚类最后的聚点，图3.14最右边一列显示的是各样品与最后聚点之间的欧式距离。

图3.12　初始聚点

图3.13　迭代过程

图3.14　各类的成员

图3.15　最后的聚点