分层聚类一开始将每个样品看成是一类或一簇（cluster），然后从低到高创建一个聚类的层次。其中，最低层次的簇合并在一起创建下一个较高层次的簇；这一层次的簇再合并在一起，进一步创建更高层次的簇。聚类时存在一种极端情况，以样品聚类为例，聚类后可能形成与样品数量一样多的簇，在这种情况下，簇内的样品之间极为相似（因为簇内只有一个样品），并且一个簇确实不同于其他的簇。然而，这种聚类没有任何意义，因为聚类的目的就是要发现样品中有用的模式并对这个模式进行概括，使分析对象更容易理解。任何形成与样品数一样多的簇的聚类算法对解决问题没有任何帮助，关于聚类的重要一点就是应该形成比原先样品数量更少的簇。在分层聚类中，采用不同的类间距离对同样的样品对象进行聚类会形成不同的聚类效果；应当恰好形成多少簇还依赖于对分层聚类图（谱系图）的分析和解释，这是一个主观的过程。分层聚类适合样品或变量较少的环境，其优势在于它们允许最终用户从许多簇或某些簇中做出选择，形成对分析问题有益的模式。

这里重点讨论样品的聚类，即Q型聚类，关于变量的分层聚类可类似讨论。对于Q型聚类，是按照类间距离从小到大进行聚类，因此，Q型聚类的关键是要定义类与类间的距离。

3.3.3.1　类间距离

为简单起见，以i，j分别表示样品xi，xj，以dij代表距离d（xi，xj）。Gp，Gq分别表示两个类，设它们分别含有np，nq个样品。若类Gp中有样品x1，x2，…，xnp，则其均值为：

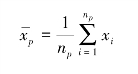
称为类Gp的重心。

类的形式与形状多种多样，因而类与类间的距离比样品间的距离复杂。下面分别介绍几种类间距离的定义与计算方法。类Gp与Gq之间的距离记为Dpq。

（1）最短距离。

即用两类中样品之间的距离最短者作为两类距离。

（2）最长距离。

即用两类中样品之间的距离最长者作为两类距离。

（3）类平均距离。

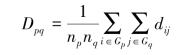
即用两类中所有两两样品之间的距离平均作为两类之间的距离。类平均距离还可用下式定义：

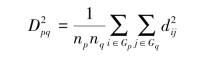
即用两类中所有两两样品之间的平方距离的平均作为两类之间的平方距离。

（4）重心距离。

其中分别是Gp，Gq的重心，这是用两类的重心之间的距离作为两类距离。

（5）离差平方和距离。

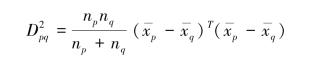
离差平方和距离是由Ward提出的，其思想来源于方差分析。

3.3.3.2　分层聚类法的步骤

（1）各样品单独自成一类，则n个样品开始时作为n个类，计算两两之间的距离，构成一个对称距离矩阵：

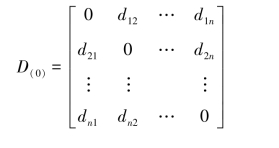
此时，Dpq＝dpq。

（2）选择D（0）中的非对角线上的最小元素，设这个最小元素是Dpq。此时，Gp＝{xp}，Gq＝{xq}。将Gp，Gq合并成一个新类Gr＝{Gp，Gq}。在D（0）中消去Gp，Gq所对应的行与列，并加入由新类Gr与剩下的其他未聚合的类间的距离所组成的一行和一列，得到一个新的距离矩阵D（1），这是一个n－1阶方阵。

（3）从D（1）出发重复步骤（2）得D（2）。此时，可能存在两种情况：或者是第三个样品加入到已有两个样品的类中，或者是另两个样品合并成一个新类。

（4）再由D（2）出发重复上述步骤。在这期间的每个步骤中，或者是一个样品加入到已存在的类中，或者是两个样品合并成一个新类，或者是两个已存在的类合并成一个新类。一旦一个类形成，不能再划分而只能与其他类合并，直到n个样品聚为1个大类为止。

（5）在合并过程中要记下合并样品的编号及两类合并时的水平（即距离）并绘制分层聚类图。(www.daowen.com)

3.3.3.3　分层聚类法应用分析

用分层聚类法聚类时，聚多少类为合适是一个很实际的问题。一个较好的聚类应该在类内各样品尽可能相似的前提下，使得类的个数尽可能少。对于相同的样品对象，分层聚类在具体操作中，可采取不同的类间距离进行计算，并得到不同的分类结果。哪个结果更能反映样品对象本身的客观分类，这种判断的正确与错误将直接决定分层聚类法在实际应用中的价值。下面举一个实际应用的例子。

表3.7是某年度20个代表性地区农村居民家庭平均每人生活消费现金支出情况。

表3.7　某年度20个地区农村居民家庭平均每人生活消费现金支出　（元）

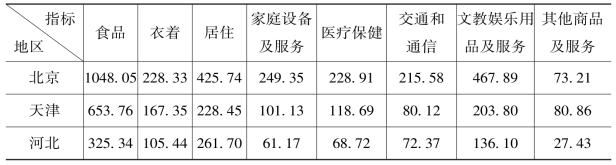
续表

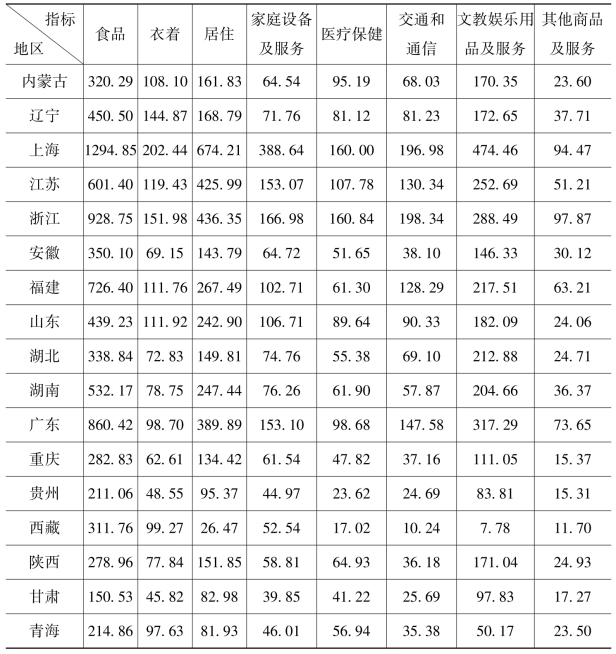
为了分析这个多变量问题，下面利用SPSS的聚类分析对各地区进行分类。在层次聚类的参数选择中，选择按样品聚类；聚类指标为食品、衣着、居住、家庭设备及服务、医疗保健、交通和通信、文教娱乐用品及服务、其他商品及服务；样品间的距离采用欧式距离；类间距离分别采用最短距离、最长距离和重心距离，不同的类间距离算法适合不同的聚类形状，在不了解聚类形状之前，可尝试多种类间距离算法并对不同的分类效果进行比较分析。

（1）最短距离法。

图3.5是聚类谱系图。

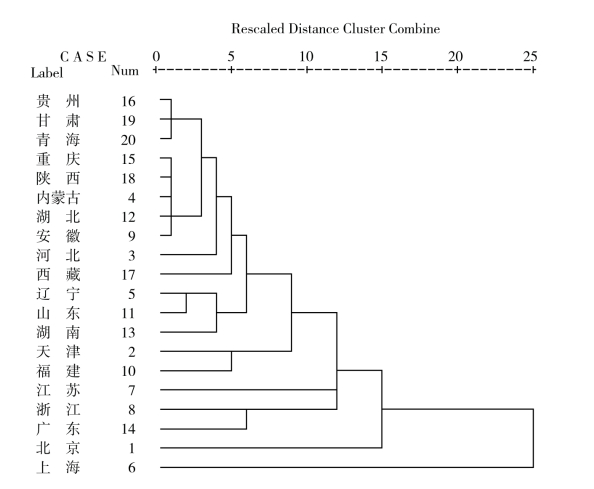
图3.5　谱系图

谱系图是一个形象地表达聚类过程的可视化层次图。从图中，能够很容易地观察出不同样品间的聚类，例如样品上海与前面19个样品聚成的簇在最后一步形成最高层次的簇。图中的竖线表示聚类时的距离，最上面显示比例调整后距离的大小。相邻两次聚类距离的差值越大，则说明前一次聚类后没有必要再进行后一次聚类，这是根据谱系图进行主观分类的依据。图中左边显示了样品的标签和编号。为了掌握更详细的聚类过程，可进一步参考图3.6中的细节描述。

在图3.6中，“Stage”代表聚类的步骤，20个样品聚类共用了19步。“Cluster Combined”代表每一个聚类步骤中合并的两类，如第一步代表编号16（贵州）和19（甘肃）进行聚类，聚类后的类用编号16表示。“Coefficients”代表最短距离算法下类间的欧式距离，如贵州和甘肃的欧式距离为66.047。图中右边几列的信息代表相应类第一次出现和下一次出现的步骤。

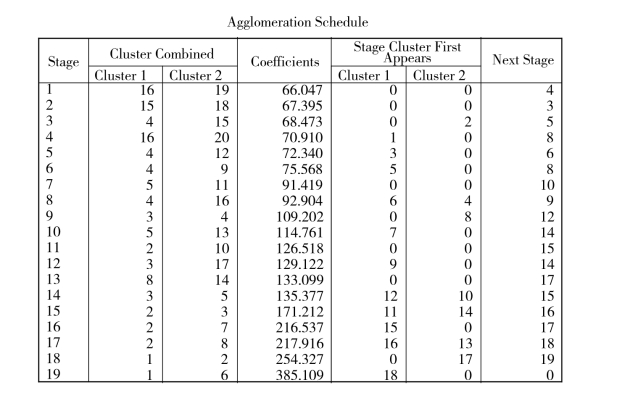
图3.6　聚类过程

在上图中，从第18次聚类到第19次聚类，“Coefficients”具有最大的跨越，这对应着图3.5中样品上海与前面19个样品聚成的簇最后形成最高层次的簇。因为距离相差最大，可先从这里开始将原样品分成两类：上海为一类，其余所有的样品为一类。是否还要继续分类依赖于实际的应用环境，最终形成的分类是一个主观分析的结果。另外，在不了解聚类形状的情况下，这样的分类是否反映了样品分类的客观本质，还应对其他类间距离算法下的分类结果进行分析和比较，才能最后做出决定。

（2）最长距离法。

在最长距离算法下得到的谱系图见图3.7，聚类过程见图3.8。

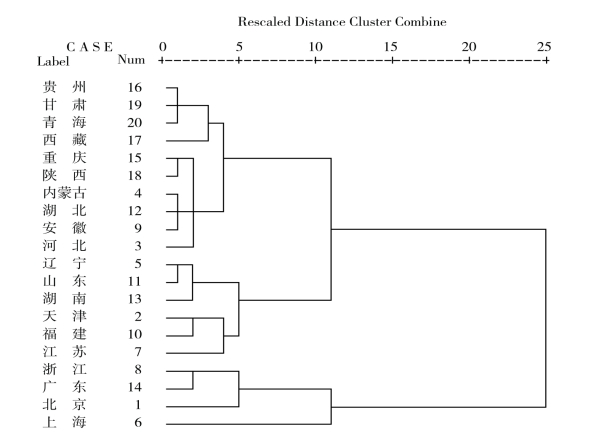
图3.7　谱系图

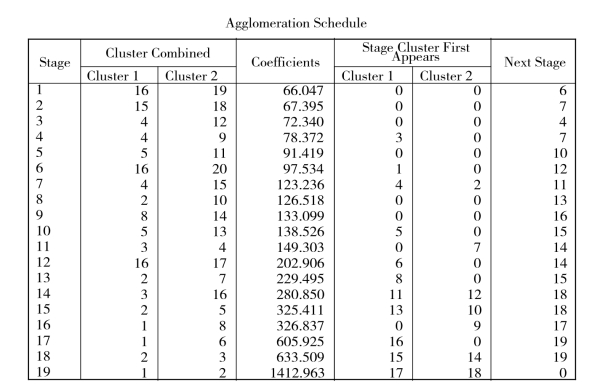
图3.8　聚类过程

通过同样的分析，可首先将原样品分成两类：一类是农村居民家庭平均每人生活消费现金支出较高的地区，它们是浙江、广东、北京、上海；另一类是农村居民家庭平均每人生活消费现金支出较低的地区，它们是除以上四个地区以外的所有地区。

（3）重心距离法。

在重心距离算法下得到的谱系图见图3.9，聚类过程见图3.10。

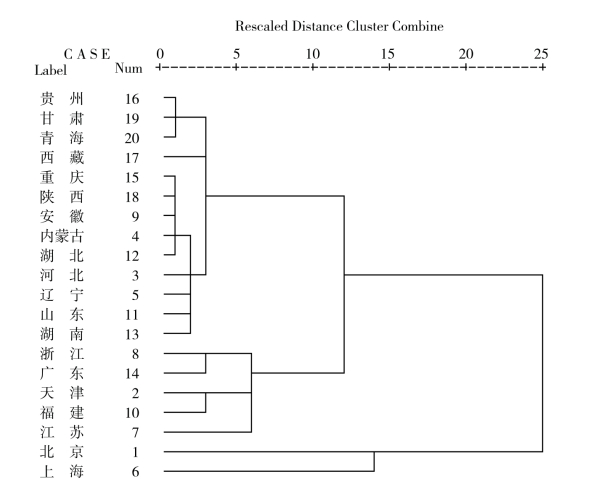
图3.9　谱系图

同样，可先将原样品分成两类：一类是农村居民家庭平均每人生活消费现金支出较高的地区，它们是北京、上海；另一类是农村居民家庭平均每人生活消费现金支出较低的地区，它们是除以上两个地区以外的所有地区。

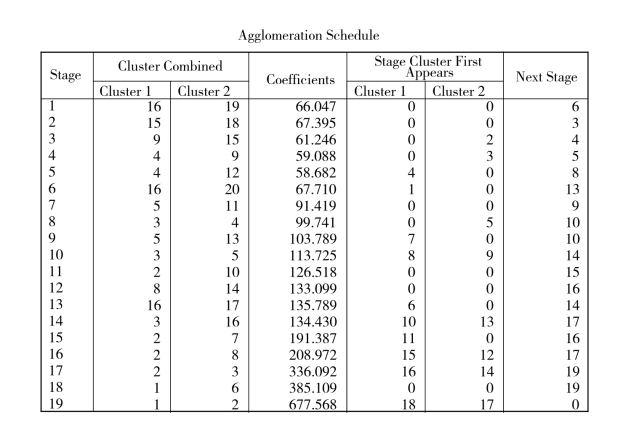
图3.10　聚类过程