回归分析在信息分析中应用广泛。以一元回归分析为例，对于两个变量x和y，若通过观测或实验可得到n组样本数据，则可将回归分析应用于如下两种情形：一是这两个变量本身就具有某种相关关系（如线性关系），但由于存在各种观测或实验误差使之不具备这种关系，通过回归分析的应用，可使该关系得到恢复和体现，从而用于预测和控制；二是这两个变量本身不具有某种相关关系，此时，可尝试着借助回归分析的应用，通过抓主要矛盾和矛盾的主要方面的做法，使这两个变量近似地具有某种关系，以便于进行预测和控制（当然，对于任意两个变量，并非总能尝试成功）。下面，我们以某年度中国各地区城镇居民平均每人全年可支配收入和消费性支出两个变量为例（见表3.3），说明回归分析的实际应用。

表3.3　某年度各地区城镇居民平均每人全年可支配收入和消费性支出　（元）

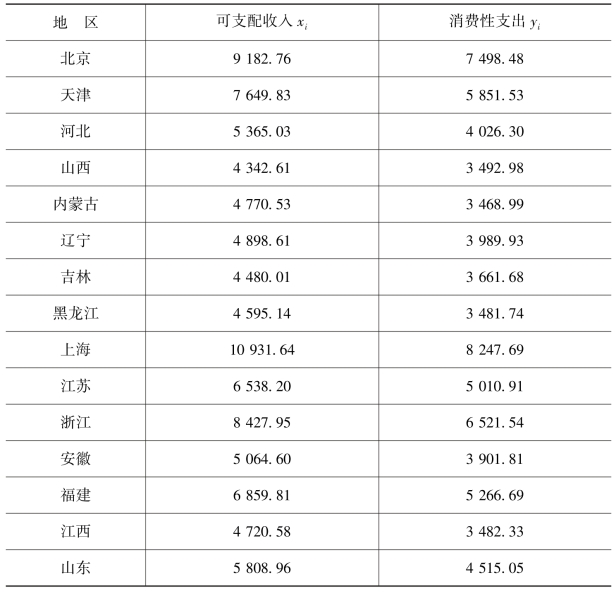
续表

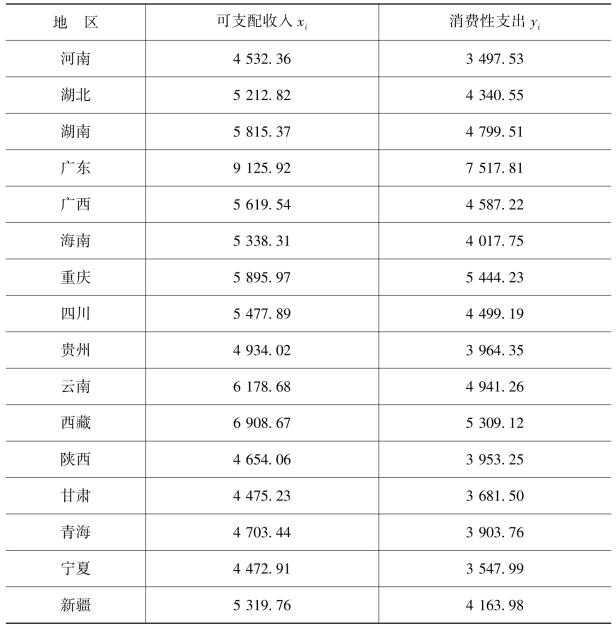
下面利用社会科学统计分析软件SPSS对上表中的数据进行回归分析，结果如下。

3.2.3.1　作散点图

先通过散点图（见图3.4）对变量进行观察，从图中易知，可支配收入与消费性支出间应该存在线性关系。

图3.4　散点图

3.2.3.2　方差分析

方差分析的结果见表3.4。

表3.4　方差分析SPSS输出结果(www.daowen.com)

查自由度为1，29的F分布临界值表得：

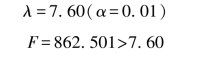
所以可支配收入与消费性支出之间具有强线性相关关系。

回归方程为：

消费性支出＝0.772×可支配收入＋126.005

3.2.3.3　预测值与残差

通过SPSS，可以按要求输出消费性支出的预测值、残差和标准化残差，见表3.5。其中，。

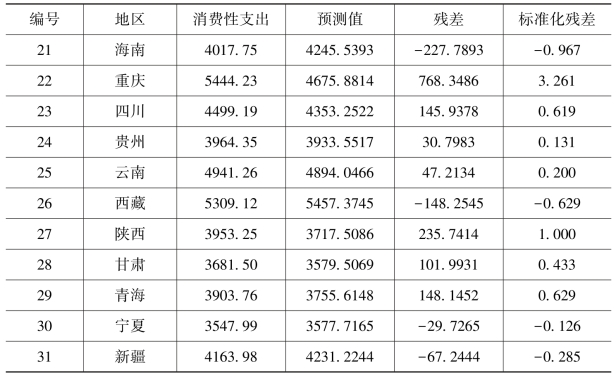
表3.5　消费性支出的预测值及残差

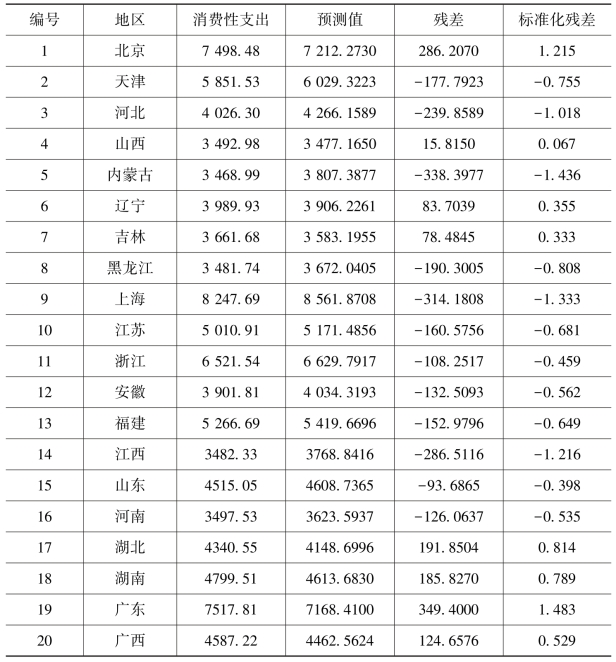
续表