3.2.1.1　一元线性回归方程参数的求解

信息分析的对象及其影响因素通常牵涉许多变量，这些变量之间常常存在各种各样的相关关系，如价格与需求、收入与支出、投资与收益等。一元线性回归分析法主要用于研究两个变量之间的线性相关关系。

对于有一定联系的两个变量x和y，若通过观测或实验得到n组样本数据：

将以上各对数据在同一平面上画散点图，发现这些点虽然是散乱的，但大体上散布在某条直线的周围（见图3.3），则表明这两个变量之间大致呈线性关系。可用数学公式表示为：

它代表平面上任意一条直线l。

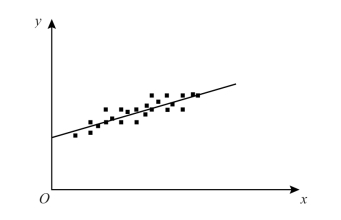
图3.3　一元线性回归示意图

设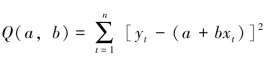。为了书写方便，把“”简化为“∑”。

Q（a，b）定量地描述了直线l跟以上n个点的总的远近程度，它随不同的a与b而变化，是a、b的二元函数。

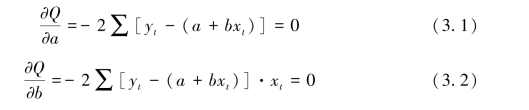
求解得：

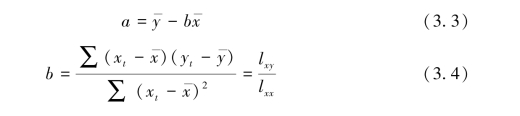
数学上可以证明，式3.3和式3.4确定的a、b确实使Q（a，b）达到最小。由于Q（a，b）是n个平方之和，所以“使Q（a，b）最小”的方法称为最小二乘法。

求出了a、b，也就求出了直线l：，这便是x、y之间的经验公式即回归方程，b为回归系数。

3.2.1.2　回归方程效果的检验

在求出回归方程之后，是不是就可用它来进行预测和控制了呢？要注意的是，我们从任意一组数据（x1，y1），（x2，y2），…，（xn，yn）出发，按式3.3和式3.4都可建立起上述回归方程，但y与x是否真的有近似的线性相关关系？这还有待进一步检验和判明。

（1）平方和分解公式。

对于任意n组数据（x1，y1），（x2，y2），…，（xn，yn），容易证明：

在上式中，是y1，y2，…，yn这n个数据的偏差平方和，它的大小描述了这n个数据的分散程度，记作lyy。容易证明，的平均数也是所以就是这n个数的偏差平方和，记作U，它描述了的分散程度。是Q（a，b）的最小值，记作Q。Q是除了x对y的线性影响之外的剩余因素对y的分散性作用，这些剩余因素包括x对y的非线性影响及试验误差等，所以Q又称为剩余平方和。

通过以上分析，式3.5可表示为：

其具体含义为，y1，y2，…，yn的分散程度（lyy）可以分解为两部分，一部分是（来源于x1，x2，…，xn的分散性）通过x对y的线性相关关系而引起的分散性（U），另一部分是剩余部分引起的y的分散性（Q）。

（2）F检验。

在一般分析中，通常选用量F进行回归方程效果的检验。F为：

F体现了x与y的线性相关关系的相对大小：如果F值相当大，则表明x对y的线性影响较大，就可以认为x与y有线性相关关系；反之，若F的值较小，则没有理由认为x与y间有线性相关关系。

F值究竟多大，才认为x与y间具有线性相关关系呢？

数学上可证明，在假设H0：b＝0的前提下，F服从自由度为1，n－2的F分布。这样，我们就可以得到关于F检验的一般程序：

①计算U，Q，从而得F值。

②对于给定的检验标准α，查自由度为1，n－2的F分布临界值表^[8]，得临界值λ：P（F＞λ）＝α。(www.daowen.com)

③比较F值与λ值的大小。如F＞λ，则否定假设H0，可认为x、y间具有线性相关关系；否则，没有理由认为x、y间存在线性相关关系。

（3）t检验。

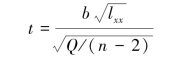
t服从自由度为n－2的t分布。t检验的一般程序如下：

①计算t值。

②对于给定的检验标准α，查自由度为n－2的t分布临界值表，得临界值λ：P（t＞λ）＝α。

③比较t值与λ值的大小。如果t＞λ，则认为x、y间存在线性相关关系；否则，没有理由认为x、y间存在线性相关关系。

3.2.1.3　可线性化的非线性回归

对于回归方程的模式是线性的情况，可直接根据式3.3和式3.4求得a、b。然而，大量的实际情况并不总是属于线性的模式，怎么办呢？一个常用而简便的方法是尽可能地将它们变为线性的模式。现将可线性化的几类非线性回归问题分述如下：

（1）指数函数模式。

线性化的方法是对式3.6两边取对数，并令

则式3.6可化为

（2）幂函数模式。

将式3.7两边取对数，并令

则式3.7可化为

（3）双曲线模式。

令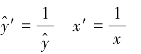

则式3.8可化为

（4）对数函数模式。

令x′＝lnx

则式3.9可化为