数据压缩过程一般可由图9.13表示

图9.13　数据压缩模型

在图9.13中,U=UK=(U1U2…UK)表示离散无记忆信源U的K次扩展信源。X=(X1X2…Xn)中各随机变量Xi∈{0,1}(i=1,2,…,n)。在图9.13所示一般数据压缩系统中,信源U=UK=(U1U2…UK)的K个信源符号被压缩成X=(X1X2…Xn)的n个比特,并通过某种方式,由X=(X1X2…Xn)还原出K个信宿符号V=(V1V2…VK)。

显然,在满足保真度准则的要求下,每个信源符号至少需要几个比特来表示,这是数据压缩过程的关键性指标。根据信息率—失真函数的定义可知,这个指标与信息率—失真函数必定存在内在联系。

定理9.15　设R(D)是离散无记忆信源U的信息率—失真函数,D 是U和V每一个符号的平均失真度。若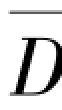 ≤D,则压缩比

【证明】　若U=(U1U2…UK)与V=(V1V2…VK)之间的平均失真度满足

因有

则就有

这表明,在图9.13中,由U=U1U2…UK到X=X1X2…Xn的压缩过程和由X=X1X2…Xn到V=V1V2…VK的还原过程所形成总的变换过程,只要最终U=U1U2…UK与V=V1V2…VK之

间满足保真度准则则对单个符号来说,一定满足保真度准则

根据离散无记忆信源的K次扩展信源U的信息率—失真函数RK(D)的定义,有

而离散无记忆信源U的信息率—失真函数R(D)与其K次扩展信源U=UK=(U1U2…UK)的信息率—失真函数RK(D)之间有

由式(9.144)、式(9.145)可得

另一方面,根据数据处理定理,有

而

因为X=(X1X2…Xn)中各随机变量Xi∈X:{0,1},所以联合熵

则由式(9.147)、式(9.148)和式(9.149)可得

则由式(9.144)、式(9.145)和式(9.150)可有

即证得压缩比

这样,定理就得到了证明。

定理告诉我们,在图9.13所示数据压缩系统中,若要求满足保真度准则KD),则表示每个信源符号至少需要R(D)比特。定理从数据压缩的角度,直截了当地指明了信息率—失真函数R(D)的内涵。

用限失真信源编码进行数据压缩的一般机制,可用图9.14表示。

图9.14　限失真信源编码进行数据压缩

设离散无记忆信源U的信源空间为

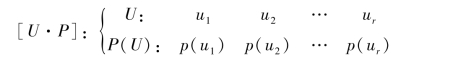
其中,

离散无记忆信源U的K次扩展信源U=UK=(U1U2…UK)有rK个长度为K的消息,其中

这rK个消息组成K维集合:{ui(i=1,2,…,rK)}

设信道的输出符号集合为V:{v1,v2,…,vs},则与离散无记忆信源U的K次扩展信源U=UK=(U1U2…UK)相应的信宿V=(V1V2…VK)有sK个长度为K的符号序列,其中

这sK个长度为K的符号序列组成K维集合:{vi(j=1,2,…,sK)}.

则把子集{u}1中所有长度为K的符号序列都表示为v1,即

若有子集{u}2,满足

则把子集{u}2中所有长度为K的符号序列都表示为v2,即

依此类推,若有子集{u}M满足

则把子集{u}M中所有长度为K的符号序列都表示为vM,即

一般来说,若有

则

其中各子集{u}i(i=1,2,…,M)是相互独立、互不相交的子集.

设长度为n的随机矢量X=X1X2…Xn中任何时刻的随机变量Xi∈X:{0,1}(i=1,2,…,n),则一共可组成2n种长度均为n的“0”、“1”序列,其中

若M≤2n,则可按某种一一对应的确定函数关系

把每一种不同的长度均为n的“0”、“1”序列,与码C:{v1,v2,…,vM}中每一种不同码字vi(i=1,2,…,M)一一对应,即有

也就是说,可以用M=2n种长度均为n的“0”、“1”序列,分别一一对应地代表M种互不相交的信源U=U1U2…UK的长度为K的消息子集{u}i(i=1,2,…,M),即

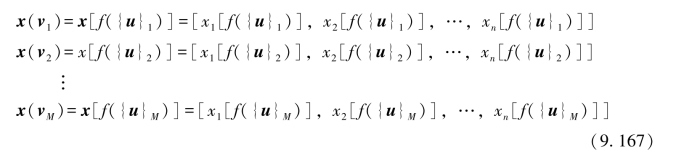
最后,M=2n种长度均为n的“0”、“1”序列可根据确定函数关系

即

一一对应地还原出相应码字vi(i=1,2,…,M),即f[{u}i](i=1,2,…,M),即有

采用式(9.156)所示信源编码C:{v1,v2,…,vM},离散无记忆信源U的K次扩展信源U=UK=U1U2…UK的每一个长度为K的消息序列ui=(ui1ui2…uiK)(i=1,2,…,rK),都可由随机矢量X=X1X2…Xn的一个长度为n的“0”、“1”符号序列来表示,即由n比特来表示.这时,离散无记忆信源U的K次扩展信源U=U1U2…UK发出的消息序列ui(i=1,2,…,rK)与信源编码C:{v1,v2,…,vM}之间的平均失真度

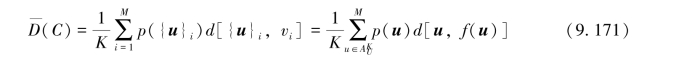(www.daowen.com)

在M=2n的情况下,数据压缩系统的压缩比就是信源U=U1U2…UK发出消息ui(i=1,2,…,rK)的长度K,与由“0”、“1”组成的随机矢量X=X1X2…Xn的符号序列长度n之比,即

【例9.8】设离散无记忆信源U的信源空间为

选用汉明失真度,即失真矩阵为

若信源U的K=7次扩展信源U=U7=(U1U2U3U4U5U6U7)的限失真信源编码C有M=16个码字,即

解:离散无记忆信源U:{0,1}的K=7次扩展信源U=U1U2U3U4U5U6U7共有2K=27=128个互不相同的长度为K=7的“0”、“1”序列组成集合.信宿V=V1V2V3V4V5V6V7同样有2K=27=128个互不相同的长度为K=7的“0”、“1”序列组成集合.在集合中选择了M=16个长度为K=7的“0”、“1”序列作为信源编码C:{v1,v2…,v16},如图9.15所示。对于每一个码字vi(i=1,2,…,M=16),在集合中,均有8个长度为K=7的互不相同的“0”、“1”序列{u}i与码字vi的汉明距离是最小的,即的等于1。因为选用的是汉明失真度,也就是说,对于每一个码字vi(i=1,2,…,M=16),在A7U集合中,均有8个长度为K=7的互不相同的“0”、“1”序列{u}i(i=1,2,…,M=16),与码字vi之间的失真度d[{u}i,vi](i=1,2,…,M=16)是最小的,即等于1,即有

则这8个“0”、“1”序列{u}i(i=1,2,…,M=16)就由码字vi来表示,即有

因为码字数M=16,故可取n=4,即有

这就是说,每一个长度为K=7的码字vi(i=1,2,…,M=16),可用X=X1X2X3X4的一个长度n=4的“0”“1”序列来表示。X=X1X2X3X4的M=2n=24=16个“0”、“1”序列为

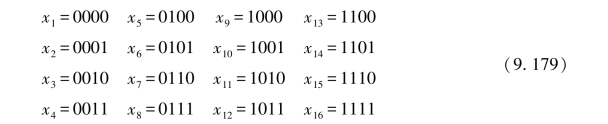
把每一个xi(i=1,2…,16)与每一个vi(i=1,2,…,16)一一对应地组成码字对(xi;vi)(i=1,2,…,16),如图9.15所示。

图9.15　编码过程

显然,由接收到的长度为n=4的“0”、“1”序列xi(i=1,2…,16),可以一一对应、唯一确定地还原出相应的码字vi=f({u}i)(i=1,2,…,M=16),再由vi还原出它所代表的8个信源U的消息序列ui(i=1,2,…16),如图9.16所示。

显然,根据上述失真信源编码方法和数据压缩机制,限失真信源编码C:{v1,v2…,v16}的平均失真度

信源U=UK=(U1U2U3U4U5U6U7)的A7U集合中的每一个子集{u}i(i=1,2,…,M)中含有8个长度为K=7的互不相同的“0”、“1”序列,除了其中一个是码字vi(i=1,2…,M)本身以外,其余(8-1)个序列与码字vi(i=1,2…,M)之间的汉明距离等于1,在汉明失真度下,{u}i(i=1,2,…,M)中的一个序列与码字vi(i=1,2…,M)之间的失真度等于零,其余(8-1)个序列与码字vi(i=1,2…,M)之间的失真度均等于1,所以

图9.16　信源消息的还原

由于信源U:{0,1}是离散无记忆等概信源,所以子集{u}i(i=1,2,…,M)中的每一个序列uil的概率分布为

由式(9.180)、式(9.181)和式(9.182),有

再考虑到离散无记忆信源U={0,1}是一个二元等概信源,则离散无记忆信源U,在满足保真度准则

的条件下的信息率—失真函数

另一方面,离散无记忆信源U的K=7次扩展信源U=U7=U1U2U3U4U5U6U7的消息是u,是长度为K=7的“0”、“1”序列,X=X1X2X3X4的“0”、“1”序列长度n=4.由此可得,限失真信源编码C:{v1,v2,…vM;M=16}的压缩比

由式(9.185)、式(9.186)可得

这个结果证实,用限失真信源编码C:{v1,v2,…vM;M=16}对离散无记忆信源U进行数据压缩,信源U的每一个符号需要的比特数,一定不小于R(D)。

【例10.3】设离散无记忆信源U的信源空间为

选定失真矩阵为

离散无记忆信源U的K=2次扩展信源U=U2=U1U2的限失真信源编码

按定义,ui与vi之间的失真度

则ui(i=1,2,…,9)与码字v2和v3的失真度分别为

续表

所以,首先可确定

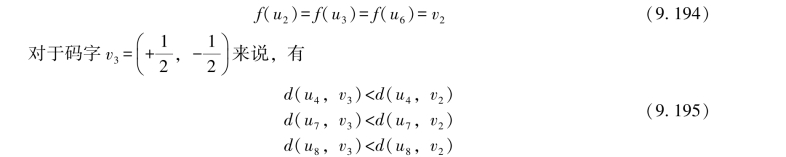
所以,又可确定

因为

所以,对于u1,u5和u9来说,选择码字v2和v3对平均失真度都是相同的效果,若选择

这样,可得到码字v2,v3和信源序列ui(i=1,2,…,9)的对应关系,如图9.17所示。

图9.17　码字与信源序列对应关系

因为码C含有的码字数M=2,故可取n=1,即可有

根据上述限失真信源编码和数据压缩机制,有

因为给定信源U:{-1,0,+1}是离散无记忆等概信源,所以U的K=2次扩展信源U=U2=U1U2的每一条消息ui(i=1,2,…,9)的概率分布

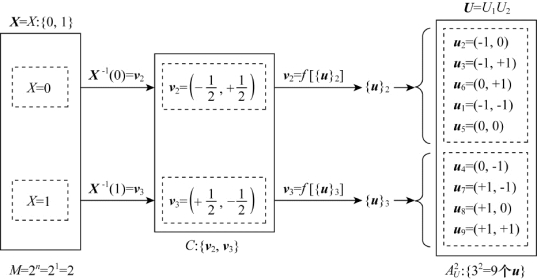
图9.18　信源消息序列的恢复

由(9.204)和(9.205)式,有

动手实践:图像的离散余弦变换

利用MATLAB工具箱中的离散余弦变换函数,对一个图像实现离散余弦变换,并求出逆变换后重构图像的均方误差。

输入:读入一幅图像。

输出:离散余弦变换结果、逆变换后重构图像和均方误差。