1.二元离散信源的R(D)函数

二元离散无记忆信源在汉明失真度下的信息率——失真函数的R(D)的计算,是离散信源信息率失真理论的基础。

定理9.13　若二元离散无记忆信源X的概率分布中的一个概率分量为ω＜,且允许失真度为D,则在汉明失真度下,信源X的信息率——失真函数

【证明】设二元离散无记忆信源X的信源空间为

(1)Dmin和R(Dmin)

根据定理9.2,由式(9.64)和式(9.65)得

由式(9.66),得满足保真度准则

的试验信道的信道矩阵

因为式(9.68)所示试验信道矩阵[P]中,每列只有一个非零元素1,所以,试验信道的疑义度

由式(9.69)、式(9.70)和式(9.64),证得

(2)Dmax和R(Dmax)

根据定理9.6,由式(9.64)和式(9.65)得最大允许失真度

显然,式(9.75)所示的信道矩阵的试验信道的噪声熵

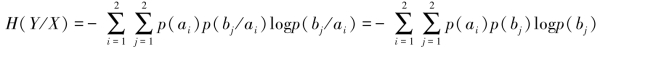
由式(9.76)、式(9.77),证得

(3)R(D)

在图9.1所示的通信系统中,设给定离散无记忆信源:X:{a1,a2,…,ar}的概率分布为P(X):{p(ai)(i=1,2,…,r)},试验信道的传递概率P(Y/X):{p(bj/ai)(i=1,2,…,r;j=1,2,…,r)},在汉明失真度

下的平均失真度

由式(9.79)和式(9.80)可改写为

在式(9.81)中,传递概率

就是信道把符号ai(i=1,2,…,r)错误地传递为符号bj(j≠i)的错误传递概率,所以概率

是信道把符号ai(i=1,2,…,r)传递为各种可能的错误概率bj(j≠i)的概率的总和,即信道传递输入符号ai(i=1,2,…,r)的总的错误概率。由式(9.81)可知,在汉明失真度下,平均失真度就等于信道的平均错误传递概率Pe,即

这是汉明失真度的一个重要特点。由此,汉明失真度又称之为“错误概率失真度”。

在阐明了汉明失真度这一重要的特点后,再回到如何导出R(D)的一般表达式这个核心问题上来。

根据式(9.84),若选择允许失真度为D,则保真度准则就为

根据Fano不等式,由式(9.85),得

式(9.86)表明,在汉明失真度下,满足保真度准则 =D的试验信道的疑义度H(X/Y)存在最大值

则根据信息率——失真函数R(D)的定义,有

式(9.88)是图9.1所示通信系统,在汉明失真度下的信息率——失真函数R(D)的一般表达式。对于概率分布为(ω,1-ω)的二元(r=2)离散无记忆信源X来说,在汉明失真度下的信息率——失真函数

其函数曲线如图9.5所示。

图9.5　二元离散无记忆信源信息率——失真函数曲线

(4)R(D)的试验信道

定理要得到完整的证明,还必须回答这样一个问题,即能不能找到一个试验信道,其平均失真度 =D,且平均交互信息量I(X;Y)达到信息率——失真函数R(D)=H(ω)-H(D)

在图9.1所示一般通信系统中,若选择汉明失真度

在式(9.92)中,

是反向信道传递Y=bj(j=1,2,…,s)的错误传递概率pej(j=1,2,…,s),式(9.92)可改写为

而式(9.92)既表明正常信道的平均失真度,又表示反向信道的平均失真度。所以式(9.92)、式(9.93)、式(9.94)表明,在汉明失真度下,反向信道的平均失真度,同样等于平均错误传递概率Pe。由式(9.94)可知,平均错误概率Pe可用随机变量Y的概率分布P(Y):{p(bj)(j=1,2,…,s)}和后验概率P(X/Y):{p(ai/bj)(i≠j)}来表示。这就意味着,可通过选择适当的后验概率p(ai/bj)(i≠j),使“反向信道”成为满足保真度准则=D的试验信道。

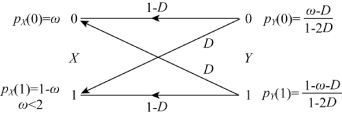
图9.6　反向试验信道

对概率分布为(ω,1-ω)的二元(r=2)离散无记忆信源X,若允许失真度为D,设反向试验信道(图9.6)的传递概率分别为:

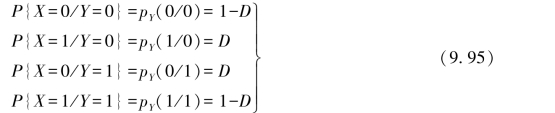
由式(9.92)可知,反向试验信道的平均失真度

这表明,图9.6所示反向试验信道满足保真度准则

由式(9.95),可得图9.6所示反向试验信道的条件熵

另一方面,因为式(9.86)是在汉明失真度下普遍成立的,所以对于二元(r=2)离散无记忆信源X,式(9.86)可改写为

由式(9.98)和式(9.97)可知,图9.6所示反向试验信道的条件熵H(X/Y),已达到最大值,即

则其平均交互信息量I(X;Y)达到最小值

则根据信息率——失真函数R(D)的定义,图9.6所示反向试验信道就是达到信息率——失真函数

的试验信道。

最后,令反向试验信道的输入随机变量Y的概率分布

则

由X的概率分布(ω,1-ω)可得

即解得

和

这表明,以式(9.105)、式(9.106)作为输出随机变量Y的概率分布,以式(9.95)作为信道传递概率P(X/Y)的反向试验信道,就是给定信源X在汉明失真度下的信息率——失真函数R(D)的试验信道。

由式(9.63)清楚地看到,当允许失真度D=Dmin=0,即不允许失真时,为了满足保真度准则 =Dmin=0,信源X必须输出全部的信息量,即R(0)=H(ω);当允许失真度为D(0＜D＜ω)时,为了满足保真度准则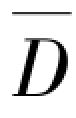=D,则信源X必须输出的最小信息量可由原来的H(X)=H(ω)下降到R(D)=H(ω)-H(D),即由于允许失真D,使信源X的最小输出信息率压缩了H(D)。

【例9.6】设二元离散无记忆信源X的信源空间为

规定汉明失真度,即失真矩阵为

解:(1)由式(9.66),有

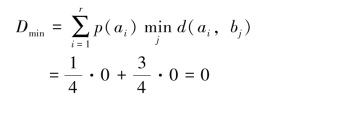
由式(9.71),有

(2)由式(9.72),有

由式(9.78),有

(3)由式(9.89),有

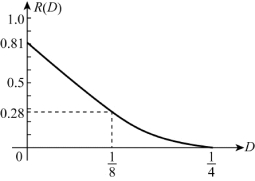
图9.7　R(D)函数曲线

(4)由式(9.95)可知,达到的反向试验信道的传递概率分别为

图9.8　反向试验信道

由式(9.105)和式(9.96)得随机变量Y的概率分布

(www.daowen.com)

2.等概离散信源的R(D)函数

等概离散无记忆信源,是一种应用广泛且比较典型的离散信源。在汉明失真度下,求解等概离散无记忆信源的信息率——失真函数,是离散信源的信息率失真理论中经常会遇到的课题。

定理9.14　在汉明失真度下,若D为允许失真度,则r元等概离散无记忆信源X的信息率——失真函数

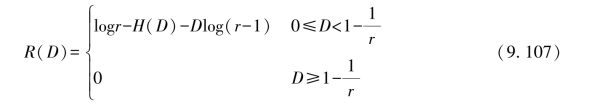
【证明】设r元等概离散无记忆信源X的信源空间为

规定汉明失真度

即失真矩阵为

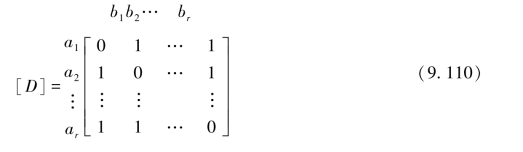
(1)Dmin和R(Dmin)

由式(9.108)和式(9.109),根据定理9.2,得

即试验信道的信道矩阵为

就是信息率——失真函数R(Dmin)=R(0)。

因为式(9.113)信道矩阵[P]中每列只有一个非零元素1,所以其后验概率

试验信道的疑义度

由式(9.114)、式(9.116)可得

(2)Dmax和R(Dmax)

由式(9.108)和式(9.109),可得

BDmax中所有试验信道都有相同的平均交互信息量

根据信息率——失真函数R(D)的定义,可得

(3)R(D)

由式(9.102)可知,在汉明失真度下,平均失真度 等于信道的平均错误传递概率Pe。当选择允许失真度

时,满足保真度准则 =D的试验信道,都有

另一方面,Fano不等式是普遍成立的,由式(9.124),得

这表明,在汉明失真度下,满足保真度准则=D的试验信道的疑义度H(X/Y)的最大值为

这样,根据信息率——失真函数R(D)的定义,由式(9.126),可得给定信源X的信息率——失真函数

由式(9.108),式(9.127)可改写为

至此,式(9.117)、式(9.122)和式(9.128)证得,在汉明失真度下,r元等概离散无记忆信源X的信息率——失真函数

由此可得r元等概离散无记忆信源X在汉明失真度下的信息率——失真函数R(D)曲线(如图9.9所示)。

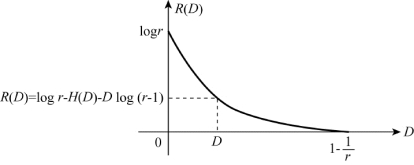
图9.9　r元等概离散无记忆信源的信息率——失真函数R(D)曲线

(4)R(D)的试验信道

定理要得到完整的证明,还必须找出一个试验信道,在满足保真度准则 =D的条件下,其平均交互信息量I(X;Y)达到式(9.129)所示R(D)。

设图9.10所示反向试验信道的传递概率为

在汉明失真度下,反向试验信道的平均失真度

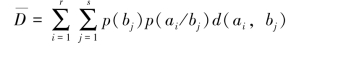
这表明,图9.10所示反向试验信道,是满足保真度准则=D的试验信道集合BD中的一个试验信道,而且平均错误概率Pe等于允许失真度D。

图9.10　R(D)试验信道

另一方面,图9.10所示反向试验信道的条件熵

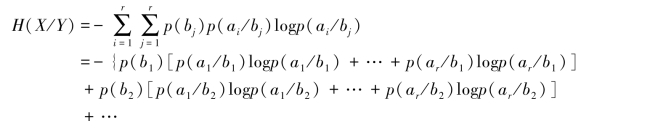
由式(9.84)可知,式(9.131)所示反向试验信道的平均失真度 等于平均错误概率Pe,则有

所以,由Fano不等式,有

这说明,图9.10所示反向试验信道的条件熵H(X/Y)已达到最大值

这个反向试验信道的平均交互信息量I(X;Y)达到最小值,即信息率——失真函数

这表明,图9.10所示反向试验信道,是达到式(9.128)所示信息率——失真函数R(D)的试验信道。

在图9.10所示的反向试验信道中,随机变量X的概率分布P(X):{p(a1),p(a2),…,p(ar)}为

由式(9.130),有

显然,当反向试验信道的输入随机变量Y的概率分布P(Y):{p(b1),p(b2),…,p(br)}选择为

时,反向试验信道的输出随机变量X的概率分布P(X):{p(a1),p(a2),…,p(ar)}就可等于给定信源X的概率分布,即

这样就证明了图9.10所示反向试验信道,是给定r元等概信源X,在汉明失真度下达到信息率——失真函数R(D)的试验信道。

综合式(9.117)、式(9.122)和式(9.128)证得,在汉明失真度下,r元等概信源X的信息率——失真函数

【例9.7】设离散无记忆信源X的信源空间为

规定汉明失真度,即失真矩阵为

解:(1)Dmin和R(Dmin)

由式(9.111),得

由式(9.117),得

(2)Dmax和R(Dmax)

由式(9.118),得

由式(9.122),有

由式(9.128),有

图9.11　R(D)函数曲线

其传递特性如图9.12所示。

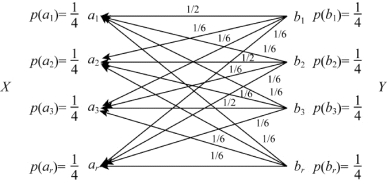
图9.12　R(D)试验信道

由式(9.139)和式(9.140)可知,为了确保信源X是等概信源,反向试验信道的输入随机变量Y的概率分布必须为

由式(9.131)可知,在汉明失真度下,反向试验信道的平均失真度

由式(9.132)可知,反向试验信道的条件熵

由式(9.135)可知,

则平均交互信息量I(X;Y)达到最小值,即信息率——失真函数