信息率失真函数R(D)就是失真小于D时所必须具有的最小信息率。本节将证明:只要信息率大于R(D),一定存在一种编码方法,使得译码后的失真小于D。

定理9.11(离散无记忆信源的限失真编码定理)　若一个离散无记忆平稳信源的率失真函数是R(D),则当编码后每个信源符号的信息率R′＞R(D)时,只要信源序列长度N足够长,对于任意D≥0,ε＞0,一定存在一种编码方式,使编码后码的平均失真度D 小于或等于D+ε。

定理9.11的含义是:只要信源序列长度N足够长,总可以找到一种信源编码,使编码后的信息率略大于(直至无限逼近)率失真函数R(D),而平均失真不大于给定的允许失真度,即D ≤D。由于R(D)为给定允许失真D前提下信源编码可能达到的下限,所以香农第三定理说明了达到此下限的最佳信源编码是存在的。

定理9.11又称为香农第三定理。可以这样来理解:N维扩展信源U=[U1U2…UN]发送序列αi和信宿接收序列βj均为N长序列,即αi∈UN,βj∈VN,并在VN空间中按照一定原则选取M=2N[R(D)+ε]个码字。信源编码时,就从M个码字中选取一个码字βj来表示信源序列αi,满足一定条件时,可以使编码后的平均失真D ≤D。此时,编码后每个信源符号的信息率为

即R′不小于信息率失真函数R(D)。需指明的是,R′和R(D)都是以“bit/信源符号”为单位。

定理9.12(离散无记忆信源的限失真编码逆定理)　若一个离散无记忆平稳信源的率失真函数时R(D),编码后信息率R′＜R(D),则保真度准则D ≤D不再满足。

限失真编码定理及其逆定理是有失真信源压缩的理论基础。这两个定理证实了允许失真D确定后,总存在一种编码方法,使编码的信息率R′可任意接近于R(D)函数,而平均失真D ≤D。反之如果R′小于R(D),那么编码的平均失真将大于D。如果用二元码符号来进行编码,在允许一定量失真D的情况下,平均每个信源符号所需的二元码符号的下限值就是R(D)。可见,从香农第三定理可知,R(D)确实是允许失真度为D的情况下信源信息压缩的下限值。

比较香农第一定理和香农第三定理可知,当信源给定时,无失真信源编码的极限值就是信源熵H(S),而限信源编码的极限值就是信息率失真函数R(D)。在给定允许失真度D之后,一般R(D)＜H(S)。

对于连续平稳无记忆信源,虽然无法进行无失真信源编码。但是在限失真情况下,有与离散信源相同的编码定理。限失真编码定理只说明了最佳编码是存在的,但是具体构造编码的方法却未涉及。实际上迄今为止尚无合适的可实现的编码方法接近R(D)这个界。

【例9.5】设一个离散无记忆信源的概率空间为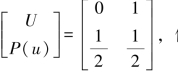假设此信源再现时允许失真存在,并定义失真函数为汉明失真。经过有失真信源编码后,将发送码字通过广义无噪信道传输,经译码后到达信宿,如图9.4所示。

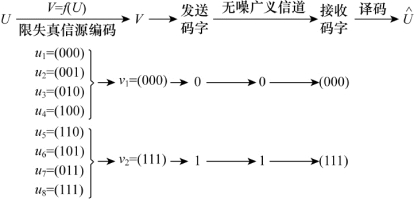
图9.4　有失真压缩编码方法示例(www.daowen.com)

(1)图9.4所示的有失真编码方案的信息传输率R′和平均失真D为多少?

(2)图9.4所示的有失真压缩编码是否为最佳方案?

解:(1)如图9.4所示的这种编码方法,把3个二元信源符号压缩成1个二元符号。因此编码后的信息率为

该编码方案中,接收序列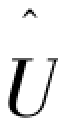与发送序列U之间有很大差异,其平均失真为

可见,图9.4所示的这种限失真编码方法压缩后信息率R′=1/3(比特/信源符号),而产生的平均失真等于1/4。

(2)根据限失真信源编码定理,总可以找到一种压缩方法,使信源输出信息率压缩到极限值R(D),当D=1/4时

显然R(D)＜R′。所以,在允许失真度为1/4时,对等概率分布的二元信源来说,本例中的压缩方法并不是最佳方案,信源还可以进一步压缩。

由上例分析可知,在允许失真度D的条件下,信源最小的、可达的信息传输率是R(D)函数,它可以作为一种衡量压缩编码方法性能优劣的尺度。