1.卷积码的距离特性

分析图8.17简单编码器生成的卷积码的距离属性,该编码器的网格图见图8.21,我们希望评估所有可能码字序列对之间的距离。对于分组码,我们关心的是该编码中这些码字序列对之间的最小距离,因为最小距离与编码的纠错能力相关。因为卷积码是群码或者说线性码,寻找最小距离可以简化为寻找所有码字序列和全0序列之间的最小距离。换言之,对于线性码,不同检测参考信息具有相同的功效。因此,为什么不选择较容易跟踪的全0序列呢?假定输入序列是全0序列,那么,感兴趣的是起始和结束状态都是00,且中间不出现00状态的路径。如果时刻ti在状态a=00合并的另一条路径的距离比全0路径的距离短,则在译码过程中全0路径将被舍弃,这样就出现了差错。换言之,当发送全0序列时,若全0序列不再幸存就会出现差错。因此,感兴趣的差错与从全0路径分叉后又与全0路径合并的幸存路径有关。为什么这条路径要再次与全0路径合并,仅仅分叉不足以表示错误吗?当然可以,但是如果仅仅用分叉表示出错,只能说明该译码器从分叉点开始,输出的都将是无用的信息。但现在需要用出错情况来量化译码器的性能,即了解译码器最容易出错的情况。通过彻底检查所有从00状态到00状态的每一条路径就可以求出上述出错情况的最小距离。首先,重画网格图如图8.30所示,在各个分支上标注与全0码字序列之间的汉明距离,而不是分支字码元。如果两个序列长度不等,则先在较短序列后附加0,以使两个序列等长,再计算它们之间的汉明距离。分析所有从全0序列分叉出去,又在某个节点第一次与全0序列合并的路径。从图8.30上可以计算出这些路径与全0路径之间的距离,有一条路径与全0路径的距离为5,它在时刻t1与全口路径分叉,在时刻t4合并;有两条路径与全0路径的距离为6,其中一条在时刻t1分叉,在时刻t5合并,另一条在时刻t1分叉,在时刻t6合并,等等。从图中的虚线和实线可以看出,距离为5的路径其输入比特是100,它与全0输入序列只有1比特的差别;同样地,距离为6的输入比特分别是1100和10100,它们与全0序列都有2位的差别。所有分叉后又合并的任意长度路径中的最小距离称为最小自由距离,简称自由距离(free distance)。此例中自由距离为5,如图8.30中粗线所示。为了计算该编码的纠错能力,将式(8.33)中的最小距离dmin用自由距离df代替,重写为

这里的[x]表示不超过x的最大整数。设df=5,图8.17中的编码器可以纠正任意两个信道错误。

网格图表示“游戏规则”,它简洁描述了某个有限状态机的所有可能状态转移及其对应的起始、结束状态。当使用纠错编码时,通过网格图还可以了解性能改善程度(编码增益)。观察图8.30中的可能的分叉-合并差错路径,可见译码器不是随意出错的,差错路径必须是允许路径之一。网格图已标明了所有这些允许路径。以这种方式对数据编码,相当于对发送信号加了限制。译码器已知这些限制,从而使得系统能更容易(使用较小的信噪比Eb/N0)地满足差错性能要求。

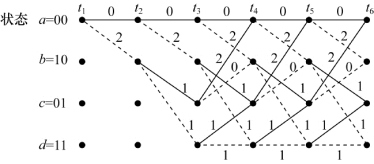
图8.30　标注了与全0路径之间距离的网格图

尽管图8.30提供了计算自由距离的直观方法,但从图8.19的状态图着手可以获得更为直接的封闭形式描述。首先,在状态图各分支上标注D0=1,D1,D2,如图8.31所示,这里的D的指数表示该分支的分支字与全0路径之间的汉明距离。节点a的自环可以省略,因为它不影响码字序列相对于全0序列的距离属性。并且,节点a可以分成两个节点(标记为a和e),其中一个代表状态图的输入,另一个代表状态图的输出。在图8.31的修改状态图上可以跟踪所有起始于状态a=00和终止状态e=00的路径。利用未定“占位符”D可以计算出路径abce(初始和结束状态都是00)的转移函数为D2DD2=D5,D的指数表明了路径上1的总累积个数,也就是该路径与全0路径之间的汉明距离。类似地,路径abdce和abcbce的转移函数都是D6,这就是路径与全0路径之间的汉明距离。状态方程如下:

其中,Xa,…,Xe都是到达中间节点的局部路径的虚拟变量。转移函数T(D),有时也称为编码的生成函数,可以表示为T(D)=Xe/Xa。求解式(8.67)中的状态方程可得

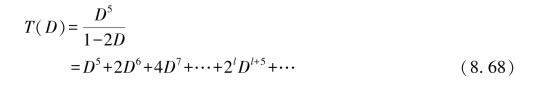
该编码的转移函数表明,与全0序列距离为5的路径只有1条,与全0序列距离为6有2条,与全0序列距离为7有4条。一般地,与全0路径的距离为l+5的路径共有2l条,l=0,1,2,…。编码的自由距离df就是T(D)展开式中最低阶项的汉明重量,此例中df=5。在评估距离属性时,转移函数T(D)不能用于较长的约束长度,因为T(D)的复杂性将随约束长度呈指数级增长。

与仅用路径距离相比,转移函数可以提供更多的信息。为状态图的每个分支引入一个因子L,则L的指数即表示任意给定的路径上从状态a=00到状态e=00的分支数。同时,在所有输入比特1产生的分支转移里引入因子N,则经过每个分支时,仅当状态转移是由输入比特1引起时,N的累积指数值增加1。对于图8.17例子中描述的卷积码,附加因子L、N,见图8.32的修正状态图,式(8.67)可以改写为

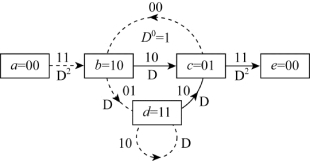
图8.31　标注了与全0路径之间距离的状态图

该扩增状态图的转移函数是

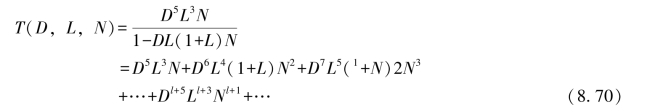
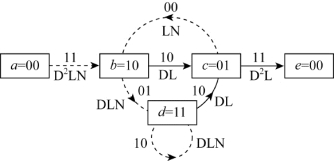
图8.32　标注有距离、长度和输入比特1个数的状态图

现在验证图8.30中描述的路径性质:有1条距离为5的路径,其长度为3,与全0路径的输入序列只有1比特的差别;有2条距离为6的路径,其长度分别为4和5,与全0路径的输入序列都有2比特的差别;有4条距离为7的路径,其中1条长度为5,2条长度为6,另1条长度为7,这4条路径与全0路径的输入序列都有3比特的差别。假定全0路径是正确路径,但是如果因为噪声干扰选择了一条距离为7的非正确路径,那么将产生3比特译码差错。

1.1　卷积码的纠错能力

由分组码内容可知,纠错能力t表示采用最大似然译码时,在码本的每个分组长度内可以纠正的错误码元的数目。但是当对卷积码进行译码时,卷积码的纠错能力不能如此简洁地描述。根据图8.25,完整的说法应当是,当采用最大似然译码时,该卷积码能在3～5个约束长度内纠正t个差错。确切的长度依赖于差错的分布,对于特定的编码和差错图样,该长度可以用转移函数来界定,具体讨论见后。

2.系统卷积码和非系统卷积码

系统卷积码是指这样的卷积码,其输入的k元组是与其关联的输出n元组分支字的一部分。图8.33显示了一个编码效率为1/2,K=3的二进制系统码编码器。对于线性分组码,将非系统码转化为系统码不会改变分组的距离属性。但对于卷积码,情况则不同,其原因就在于卷积码很大程度上依赖于自由距离。一般地,对于给定约束长度和编码效率的卷积码,将其系统化会减小最大自由距离。

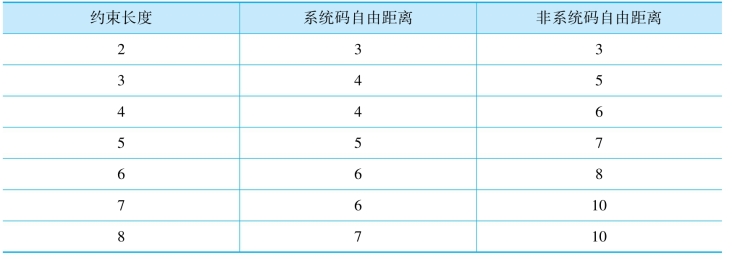
表8.5列出了K从2到8,编码效率为1/2的系统码和非系统码的最大自由距离。若约束长度更大,得到的结果差别也将更大。

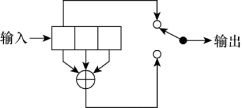
图8.33　系统卷积码编码器(编码效率1/2,K=3)

表8.5　系统码与非系统自由距离比较(编码效率为1/2)

3.卷积码中的灾难性错误传播

所谓灾难性错误(catastrophic error),是指由有限数量的码元差错引起的无限数量的已译码数据比特差错。Massey和Sain推导了卷积码出现灾难性错误传播的充要条件。对于寄存器抽头按照前面描述的生成多项式进行连接,编码效率为1/n的编码方式,发生灾难性错误传播的条件是这些生成多项式有共同的多项式因子(阶数不低于1)。例如图8.34(a)中表示的编码效率为1/2,K=3的编码器,上方生成多项式g1(X),下方生成多项式g2(X)分别为

由于1+X2=(1+X)(1+X),因此生成多项式g1(X)和g2(X)有共同的多项式因子1+X,所以,图8.34(a)中的编码器会引起灾难性错误传播(catastrophic error propagation)。

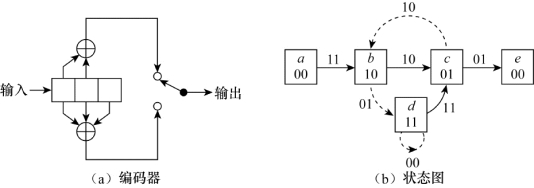
图8.34　引起灾难性错误传播的编码器

对于编码效率任意的编码器状态图,当且仅当任意闭环路径的重量为0(与全0距离为0)时,才会出现灾难性错误传播。现以图8.34为例进行阐述。图8.34(b)的状态图将状态a=00分成两个节点a和e。假定全0路径是正确路径,那么,无论在节点d的自环有多少次,不正确的路径abdd…dce上共有6个1。举例来说,对于BSC信道,若发生3个信道比特差错,结果就会选择这条不正确的路径,而在这条路径上可以有任意多个判决错误(2个加上经过的自环的次数)。经观察可见,对于编码效率为1/n的编码,若编码器的每个加法器都有偶数个连接,那么对应于全1状态的自环重量将为0,从而代码将是灾难性的。

系统码的优点在于它不会引起灾难性错误传播,因为每个闭环中至少有一个分支由非0输入比特产生,从而使每个闭环必有非0码元。不过,可以证明,仅有一小部分的非系统码(除去所有加法器都有偶数个抽头的)会引起灾难性错误传播。

4.卷积码的性能界限

可以证明,对于采用硬判决译码的二进制卷积码,其误比特率PB的上界为

其中,p是信道码元差错概率。对图8.17中的例子,令式(8.70)中的L=1,可由T(D,L,N)求得T(D,N):

并有

联立式(8.72)和式(8.74),得

(www.daowen.com)

对于加性高斯白噪声(AWGN)信道的相干BPSK调制,可以证明,误比特率的上界为

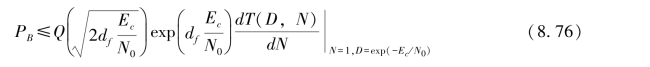
其中,

Ec/N0=rEb/N0;

Eb/N0=信息比特能量与噪声功率谱密度之比;

Ec/N0=信道码元能量与噪声功率谱密度之比;

r=k/n=编码效率。

因此,对于编码效率为1/2,自由距离df=5的编码,若采用相干BPSK调制和硬判决译码,则有

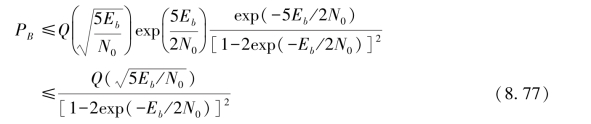
5.编码增益

编码增益是指在相同的调制方法和信道特性下,为了达到给定的差错概率,编码系统所需信噪比Eb/N0较之未编码系统的减少量,常用分贝表示。表8.6给出的编码增益上界,它是约束长度K从3到9,具有最大自由距离的卷积码,经高斯信道传输和硬判决译码后,相对于未编码相干BPSK的编码增益。由此表可见,即使只用简单的卷积码,也可以获得很好的编码增益实际编码增益将随要求的误比特率而变化。

表8.6　部分卷积码编码增益的上界

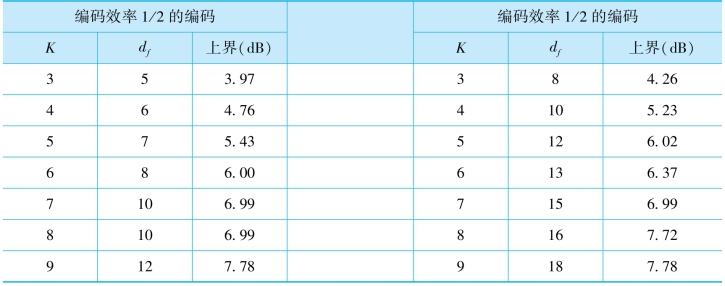
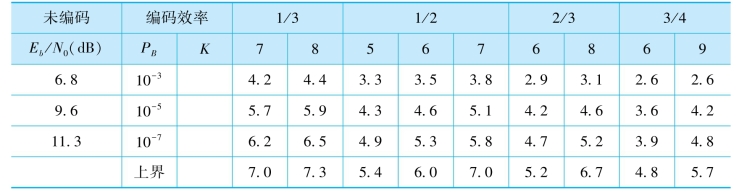
表8.7列出了经高斯信道传输、采用软判决译码、硬件实现或计算机仿真的编码,与未编码的相干BPSK相比的编码增益。未编码的Eb/N0列在表的最左边。由表可知,编码增益随误比特率的减小而增大,但不会无限上升,其上界如表中所示,用分贝表示的增益上界可以记为

其中,r是编码效率,df是自由距离。从表8.7还可以看到,对于编码效率为1/2和2/3的编码,当PB=10-7时,较弱的编码比较强编码增益和增益上界更为接近。

表8.7　软判决维特比译码的基本编码增益(dB)

一般地,维特比译码通常应用于二进制输入、硬判决或3比特量化软判决输出信道,约束长度为3～9,编码效率一般大于1/3,路径存储容量约为几个约束长度。路径存储容量指的是译码器存储的输入比特记录的长度。分析维特比译码的例子,读者也许会对固定路径存储容量大小的必要性提出疑问。由该例可看出,对于任何节点,只要该节点上仅有一条幸存路径,就可以译码出分支字。然而在实际应用中,为了实现该译码器,当对分支字进行译码时,必须伴有大量的处理过程以实现连续检测。若存在固定延迟,分支字就可在固定延迟后被译码。可以证明,对于BSC和高斯信道,从具有最小状态量度的状态回溯固定长度的路径记录(是4或5倍约束长度),足以把相对于最优译码器的性能下降限制在0.1 dB左右。图8.35给出了采用硬判决量化的维特比译码时,其差错性能的仿真结果。注意,当PB=10-5时,约束长度每增加一个单位,所需的Eb/N0降低大约0.5 dB。

6.最常用的卷积码

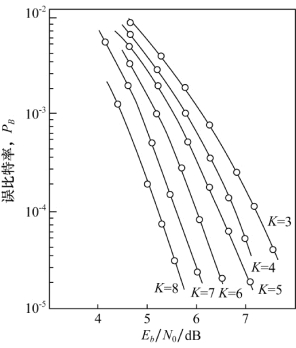
图8.35　误比特率和Eb/N0的关系曲线(BSC信道、相干BPSK、编码效率为1/2的维特比译码,具有32比特路径存储容量)

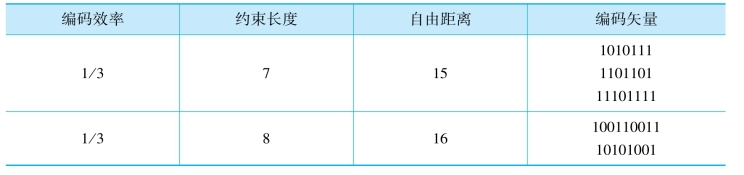
卷积码的连接矢量或生成多项式通常根据码的自由距离特性进行选择。第一准则是,对于给定的编码效率和约束长度,选择具有最大自由距离而且不会发生灾难性错误传播的编码,然后最小化最大自由距离df下的路径数,或这些路径代表的数据比特错误数。可以对自由距离为df+1,df+2的路径数或比特错误数采用上述过程进步细化,直至仅剩一个或一组编码。Odenwalder按照上述准则得到了编码效率为1/2,K=3到9,以及效率为1/3,K=3到8的最常用编码,如表8.8所示。表中的连接矢量,表示卷积码编码器相应的各级与加法器之间是否存在(1或0)抽头连接,连接失量最左边的数据项对应了编码寄存器最左端一级。值得注意的是,这些连接矢量都可以反转(左右交换)。在维特比译码情况下,反转连接得到的编码和原连接具有相同的距离参数,因此也具有相同的性能,如表8.8所示。

表8.8　短约束长度的最佳卷积码(编码效率为1/2、1/3)

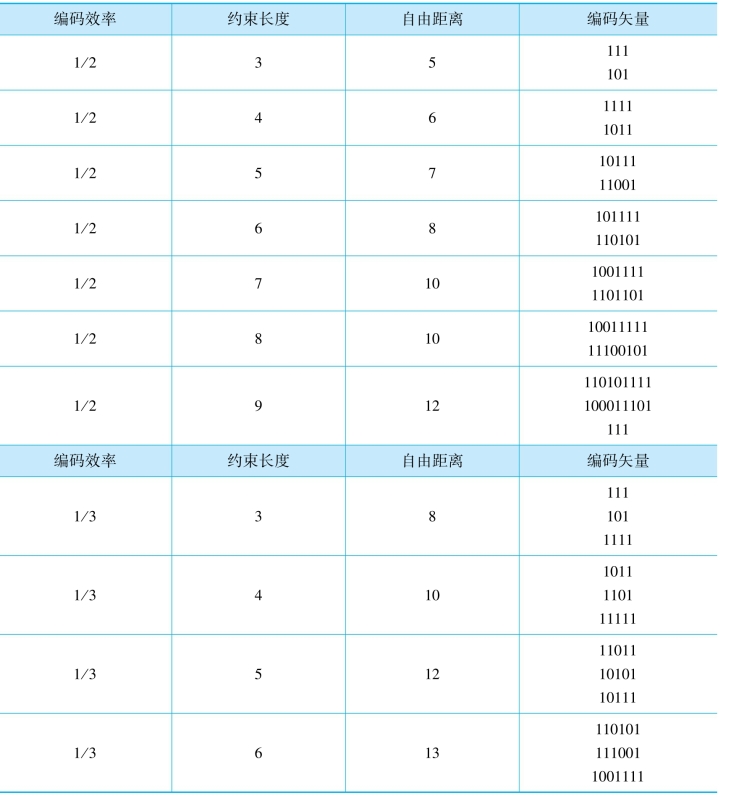
续表

实践:编码信道下的通信系统仿真

这是一个综合性的大型实验,通过搭建一个包括信源、信源编译码器、信道、信道编译码器等各模块在内的仿真通信系统,使读者能够加深对本课程各个重点章节的理解,更好地掌握通信的本质意义。

说明:

由于搭建一个完整通信系统的工作量较大,所以本实验可以使用Matlab等仿真工具。下面分别描述系统中各模块的需求。

①离散信源:能以指定的概率分布(p,1-p)产生0,1符号构成的二进制信源符号序列。

②信源编码器:信源编码器的输入是上一步产生的二进制符号序列。要求:能选择使用无编码(直通)、二进制香农编码、二进制霍夫曼编码、二进制费诺编码这四种编码方式中的任何一种。

在上一步指定信源的概率分布后,就可以马上生成这三种编码的码表,实际的编码工作只是查表而已。当然,直接对上一步指定的信源进行编码是不合适的,需要先进行信源的扩展,换句话说,需要确定信源分组的长度。这个长度N也是本系统的一个重要参数,是在系统运行之前由用户输入的。

③信道编码器:信道编码器的输入是信源编码器输出的二进制符号序列。编码方式要求能选择使用无编码、三次重复编码、Hamming(7,4)码这三种信道编码方式中的任何一种。

信道编码器是个简单的一一对应的函数转换模块,没有额外的控制参数,可以事先实现这三种编码器,统一其输入输出格式,运行时按照指定的类型直接使用即可。

④信道:其输入是信道编码器输出的二进制符号序列。经过传输后输出被噪声干扰和损坏了的二进制符号序列。要求能够模拟理想信道、给定错误概率p的BSC以及给定符号0、1各自错误概率p、q的任意二进制信道。

⑤信道译码器:由于信源经过信源编码器和信道编码器后的统计特性难以明确给出,所以此时理想译码器准则无法实施。因此,根据第四步给出的信道统计特性,采用极大似然译码准则进行译码。

⑥信源译码器:在第二步确定信源编码器后,即可同时确定信源译码器。信源译码器的工作仅仅是简单的查表。

要求:

(1)输入:各模块的相关参数。

(2)输出:信源产生的原始符号序列、信源译码器输出的符号序列、信道编码后的信息传输效率、整个通信过程的误比特率(BER)以及信道编译码过程中产生的误码率(BLER)。

提示:

(1)本实验中的信源模块部分都会用到随机数的产生。各种编程语言基本都提供了这个功能。

(2)Matlab是一个优秀的系统仿真软件,而Simulink是Matlab中最著名的通信工具箱。上述实验要求中的很多功能有Matlab或Simulink已经实现并提供了方便的调用接口。例如二进制对称信道,在Matlab中就有一个bse()函数完成了这个功能。同学们在设计、开发这个实验前应该花一些时间先熟悉Matlab及Simulink。