1.最大似然译码

如果所有的输入信息序列等概,则通过比较各个条件概率,也称为似然函数P(Z,选择其中的最大者,就可以得到具有最小差错概率的译码器,这里的Z是接收序列,U(m)是可能的发送序列如果满足如下公式,译码器就选择U(m′):

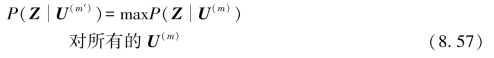
上式的最大似然概念是判决理论的基本内容;当具备各种可能性的统计知识时,它是“常识性”的判决方法的正式表式。二进制解调仅涉及两个等概的发送信号,s1(t)或s2(t),因此,给定一个接收信号,二进制最大似然判决准则为:如果

则判决发送信号为s1(t);否则,判决发送信号为s2(t)。参数z代表z(T),即在每个信号持续时间t=T时刻末尾的接收器的预检测值。不过,将最大似然准则用于卷积码译码时,必须注意到卷积码具有记忆性(接收序列代表当前比特和此前若干比特的叠加),因此,应用最大似然准则对已经卷积编码的比特译码时,应选择最大似然序列,如式(8.57)所示。通常发送的码字序列有多种可能,以二进制编码为例,含有L个分支字的序列就有2L种可能。所以,按照最大似然准则,如果某发送序列U(m)的似然函数P(Z

U(m′))比其他所有可能的发送序列的似然函数都大,那么,译码器就选择该序列为发送序列。这种最小差错概率的最优译码器(以所有发送序列等概率为前提),称为最大似然译码器(maximum likelihood decoder)。似然函数通常已给定或根据信道特性计算得到。

假定噪声是零均值的加性高斯白噪声,而且信道无记忆性,即噪声独立地影响各个码元。编码效率为1/n的卷积码的似然函数为

通常对最大似然函数取对数,从而用加法代替乘法,以简化计算。可以利用这种变换的原因是,对数函数是单调递增函数,不会改变原来码字选择的最终结果。对数最大似然函数定义为

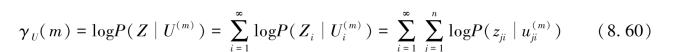
译码问题现在转化为从图8.20的树状图或者图8.21的网格图上选择一条路径,使γU(m)最大的问题,树状图和网格图都可用于卷积码的译码。在编码的树状图表示中没有考虑支路的合并,对于二进制编码,L个分支字组成的码字序列有2L种可能。用最大似然准则对某个接收序列进行译码时,若使用树状图,则需要彻底比较与所有可能发送的码字序列相对应的2L个累积对数似然函数值,因此,用树状图进行最大似然译码并不实际。从下一节的描述中可以知道,使用网格图可以构造出实际可行的译码器,它能够抛弃最大似然序列不可能经过的路径,译码路径从幸存路径(surviving path)中选取。由这种译码器得到的译码路径和前述彻底比较型的最大似然译码器所得的译码路径相同,因此也是最优的。同时,因为它能够较早抛弃不可能路径,所以降低了译码的复杂性。

卷积码结构、最大似然译码以及編码性能的详细介绍见参考资料。还有一些算法可以得到与最大似然译码接近的结果,如序贯算法和门限算法。这些算法分别适用于某些特定的应用,但都是次最优的。维特比译码算法(Viterbi decoding algorithm)采用的是最大似然译码准则,因此是最优的。但这并不表示维特比算法对一切应用均是最好的,它还受到硬件复杂性的严重限制。

2.信道模型:硬判決和软判决的比较

在介绍最大似然判決准则的算法之前,先描述一下信道特性。卷积码的码字序列U由分支字组成,每个分支字又由n个码元组成,码字序列可以看成一个无穷长的比特流,这一点与分组码恰恰相反,分组码中的源数据和码字都分成大小固定的组。图8.15中的码字序列从卷积码编码器送入调制器,将码元转换为信号波形。调制可以是基带的(如冲被形)或者带通的(如PSK和FSK)。一般地,一次送入的L码元(L为整数)被映射为信号波形si(t),i=1,2,…,M=2l。l=1时,调制器将每一个码元映射为一个二进制波形。假设信道对传送波形的干扰是高斯噪声,受到干找的信号被接收后,先经解调器解调,再经译码器处理。

假定在一个码元间隔(0,T)内传送的二进制信号波形s1(t),s2(t)分别对应于比特1,0。接收信号是r(t)=si(t)+n(t),这里的n(t)是零均值的高斯噪声。r(t)的检测分成两步:第一步,将接收波形降为单个数z(T)=ai+n0,这里的ai是z(T)的有用信号分量,n0是z(T)的噪声分量。噪声分量n0是一个零均值的高斯随机变量(Gaussian random variable),因而z(T)是一个高斯随机量,其均值为a1或a2,取决于发送信息是比特1还是比特0;第二步执行检测过程,将z(T)和门限值进行比较,从而对发送信号做出判决。z(T)的条件概率函数如图8.22所示,分别代表s1(t)和s2(t)的似然性。图8.15中的解调器将一组时序随机変量{z(T)}转換为代码序列Z,并将它发送至译码器。解调器的输出有多种构造方式。一种构造方式是硬判决实现,判定z(T)的值是0还是1,即将解调器的输出量化为两级,0和1,并送入译码器。因此译码器对解调器做出的硬判决进行处理,所以这种译码称为硬判决译码(hard-decision decoding)。

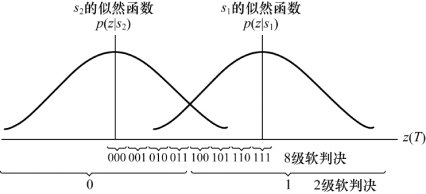
图8.22　硬、软译码判决

解调器的结构也可以是将两个以上的z(T)量化值馈送给译码器,这样可以为译码器提供比硬判决更多的信息。当解调器的输出量化级超过两级时,这种译码就称为软判决译码(soft-decision decoding)。图8.22的横坐标显示了8级(3比特)量化。当解调器发送二进制硬判决给译码器时,它仅发送单个二进制码元;当解调器发送量化为8个电平的二进制软判决时,它发送给译码器3比特码字用以表示z(T)时间间隔。实际上,往译码器发送这样的3比特码字而不是单个二进制码元,相当于给译码器发送一个带有置信度(measure of confidence)的码元判决。根据图8.22,如果解调器发送111给译码器,则说明码元是1的置信度非常大;如果解调器发送100给译码器,则说明码元是1的置信度非常小。应当清楚地认识到,译码器做出的所有信息的最终判决都将是硬判决,否则,计算机的输出结果将成为:“猜测是1”,“猜测是0”,等等。解调器不做硬判决,而是发送较多的数据(软判决)给译码器,以提供译码器更多的中间信息,使其能更好地恢复信息序列(即获得比硬判决更佳的差错性能)。在图8.22中的8级软判决量度经常表示成-7,-5,-3,-1,1,3,5,7,这样的设计使得软判决易于阐释:度量的符号表示判决(例如,如果为正,则选择s1;如果为负,则选择s2),参数的幅度则表示此判决的置信度等级。图8.22中的度量表示方法的唯一好处是避免使用负数。

对于高斯信道来说,8级量化比2级量化的信噪比提高了大约2dB,这表明为了获得相同的比特差错性能,8级软判决需要的Eb/N0比硬判决低2dB。模拟装置(或无穷级量化)比2级量化的性能提高2.2dB;因此,8级量化比无穷级量化的性能损失仅约0.2dB。由于这个原因,量化级超过8级只能获得较少的性能提高。软判决译码提高性能的代价如何呢?硬判决译码时,每个码元用1比特表示;而对于8级量化软判决译码,每个码元则用3比特表示,因此,软判决在译码过程中需要处理的数据量是硬判决的3倍。可见,软判决译码的代价是译码器所需存储器的容量的增大(可能还有速度的降低)。

分组译码算法和卷积译码算法都可用于硬判决和软判决。不过,软判决译码通常不用于分组码,因为这时它比硬判决译码实现的难度大得多。软判决译码最适用于维特比卷积译码算法(Viterbi convolutional decoding algorithm),这时采用软判决仅增加少许的计算量。

2.1　二进制对称信道

二进制对称信道(BSC)是一种离散无记忆信道,它的输入和输出是二进制数据,而且具有对称的转移概率,用条件概率函数描述为

如图8.23所示。输出码元与输入码元不同的概率是p,相同的概率是(1-p)。BSC是硬判决信道的一个例子,这意味着即使解调器接收的是连续信号,BSC只允许进行硬判决,因而解调器的输出码元zji仅由两个二进制数值之一组成,如图8.15所示,其中,zji是第i个分支字Zi的第j个码元。随后解调器把序列Z={Zi}发送给译码器。

假设码字序列U(m)经码元差错概率为p的BSC信道传送,Z是相应的接收译码序列。如前所述的最大似然译码器选择标准是,选择使似然函数或其对数值最大的码字序列U(m′)。对于BSC信道,其实就相当于选择和序列Z具有最小汉明距离(minimum Hamming distance)的码字U(m′)。汉明距离是表述U(m)和Z之间距离或者接近程度的合适度量,译码器总是从所有可能的发送序列U(m)中选择和Z距离最小的序列U(m′)。

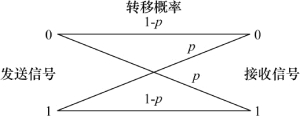
图8.23　二进制对称信道(硬判决信道)

假设序列U(m)和Z的长度都是L比特,且有dm个数据比特不同[即,U(m)和Z之间的汉明距离是dm]。由于假设信道没有记忆性,序列U(m)被转换成与它距离为dm的特定接收序列Z的概率为

其对数似然函数为

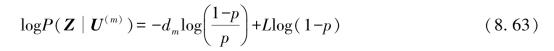
当我们对每个可能的发送序列进行计算时,等式中的最后一项都是常数。假设p＜0.5,式(8.63)可改写为

其中,A和B都是正的常数。所以,应选择这样的码字U(m′),即它与接收序列Z之间的汉明距离dm最小,这相当于最大化似然函数或对数似然函数。因而,在BSC信道的情况下,对数似然函数常用汉明距离代替,最大似然译码器将在树状图或网格图上选择这样的一条路径,使其对应的序列U(m)与接收序列Z具有最小汉明距离。

2.2　高斯信道

对于高斯信道,解调器的每个输出码元zji都是取自一个连续字符的值,如图8.15所示,因而码元zji不能标记为正确或错误判决。向译码器发送这样的软判决,相当于发送不同码元的一组条件概率。可以证明,最大化相当于最大化码字序列U(m)(由表示为双极性值的二进制码元组成)与模拟值接收序列Z的內积。因此,译码器应选择使如下表达式取最大值的码字U(m′):(www.daowen.com)

这相当于选择与序列Z具有最小欧氏距离(Euclidean distance)的码字U(m′)。尽管硬判决和软判决信道的量度不同,但它们的准则都是选择与接收序列Z最接近的码字U(m′)。为了对式(8.64)进行精确的最大化处理,译码器应该能够进行模拟值的算术运算,但这对于数字译码器而言是不切实际的,因此,需要量化接收码元zji。式(8.64)是接收波形r(t)与参考波形si(t)进行相关运算的离散形式。通常将量化的高斯信道称为软判决信道,它是前面介绍的软判决译码器的信道模型。

3.维特比卷积译码算法

维特比译码算法由维特比在1967年提出。维特比算法的实质是最大似然译码,但它利用了编码网格图的特殊结构,从而降低了计算的复杂性,与完全比较译码相比,它的优点是使得译码器的复杂性不再是码字序列中所含码元数的函数。该算法包括计算网格图上在时刻ti到达各个状态的路径和接收序列之间的相似度(measure of similarity),或者说距离(distance)。维特比算法考虑的是,去除不可能成为最大似然选择对象的网格图上的路径,即,如果有两条路径到达同一状态,则具有最佳量度的路径被选中,称为幸存路径(surviving path)。对所有状态都将进行这样的选路操作,译码器不断在网格图上深入,通过去除可能性最小的路径实现判决。较早地抛弃不可能的路径降低了译码器的复杂性。Omura在1969年证明了维特比算法实际上就是最大似然算法。注意,选择最优路径可以表述为选择具有最大似然量度的码字,或者选择具有最小距离的码字。

4.维特比卷积译码算法举例

为简化讨论,假设信道是BSC,此时汉明距离是合适的距离量度。该例的编码器如图8.17所示,编码器网格图如图8.21所示。译码器也可以用类似的网格图表示,如图8.24所示。在时刻t1从00状态开始(在发送信息前先清空译码器以提供初始状态信息)。因为该例中每个状态出发都仅有两种可能状态转移,所以开始时没有必要画出所有分支,完整的网格图结构从时刻t3起出现。结合考虑图8.21编码器的网格图和图8.24译码器的网格图,可以较好地理解译码过程的基本原理。在译码器网格图的每个时间间隔内,给各个分支标注上接收码元和编码器网格图相应各个分支上分支字之间的汉明距离(Hamming distance),这是很方便的。图8.24中的例子显示了一个信息序列m,相应的码字序列U,以及受到噪声干扰的接收序列Z=1101011001…。编码器网格图分支上的分支字表明了图8.17中编码器的特性,这对于编码器和译码器都是已知的。编码器的分支字是每个状态转移时编码器将输出的码元比特,而译码器网格图(decoder trellis)分支上的标注是由译码器连续累加得到的。具体地,当码元被接收时,译码器网格图的每个分支上标注接收码码元和编码器上各个分支字在此时间间隔内之间的相似性量度(汉明距离)。由图8.24的接收序列Z可见,在随后的时刻t1收到的码元是11。为了在译码器相应分支上标注(起程)时刻的汉明距离,观察图8.21中编码器的网格图。在此图中,从00→00状态转移伴随的输出分支字是00,但我们接收的码元是11,因此,在译码器网格图上标注00→00状态转移的汉明距离为2。00→10状态转移伴随的输出分支字是11,和在时刻t1收到的码元恰好相同,因此,在译码器网格图上标注00→10状态转移的汉明距离为0。总之,进入译码器网格图分支上的度量表明了接收序列和发送该分支对应的分支字“应该收到”序列之间的差别(距离)。实际上,这些度量描述了接收分支字和所有候选分支字之间的相关性。每个时刻ti接收信号时,按上述方法标注译码器网格图的分支。译码算法利用这些汉明距离度量在网格图上找到最大似然(最小距离)路径。

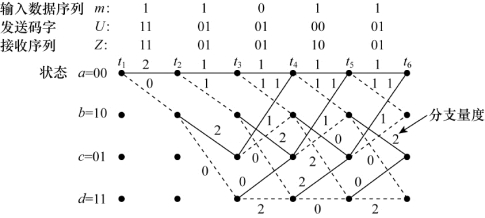
图8.24　译码器网格图(编码效率为1/2,K=3)

维特比译码的思想基础是基于如下观察:如果网格图上有两条路径在某个状态合并,在寻找最优路径时,一般总可以舍弃这两条路径中的一条。例如图8.25中,在时刻t5有两条路径在状态00合并。将某条给定的路径在时刻ti的累积汉明路径量度(cumulative Hamming path metric),定义为该路径直至ti沿途各分支的汉明距离之和。图8.25中上方路径的量度为4,下方路径的量度为1;由于下方路径与上方路径到达的状态相同,但度量值较小,因此,上方路径一定不是最优的。

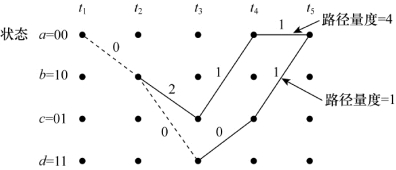
图8.25　两条合并路径的路径量度

这种思想成立的原因是编码器状态的马尔可夫性:当前状态完全概括了编码器的历史信息,以前的状态不会影响将来的状态或者将来的输出分支。

网格图中每个时刻ti上有2K-1个状态,这里的K是约束长度,每种状态都可经两条路径到达。维特比译码包括计算到达每个状态的两条路径的路径量度,并舍弃其中一条路径。在时刻ti,算法对2K-1个状态(节点)都进行上述计算,然后进入时刻ti+1,并重复上述过程。在一个给定的时刻,各状态的幸存路径量度就是该状态在该时刻的状态量度(state metric)。译码过程的前几步如下(如图8.26所示):假定输入数据序列m,码字U,接收序列Z,如图8.24所示,并假设译码器确知网格图的初始状态(这种假设在实际应用中没有必要,但可以简化解释)。时刻t1接收到的码元是11,从状态00出发只有两种状态转移方向,00和10,如图8.26a所示。状态转换00→00的分支量度是2;状态转换00→10的分支量度是0。时刻t2从每个状态出发都有两种可能的分支,如图8.26b所示。这些分支的累积量度标识为状态量度Γa,Γb,Γc,Γd,与各自的结束状态相对应。同样地,图8.26c中时刻t3从每个状态出发都有两个分支,因此,时刻t4时到达每个状态的路径都有两条,这两条路径中,累积路径量度较大的将被舍弃。如果这两条路径的路径量度恰好相等,则任意舍弃其中一条路径。到各个状态的幸存路径如图8.26d所示,译码过程进行到此时,时刻t1和t2之间仅有一条幸存路径,称为公共支(common stem)。因此,这时译码器可以判决时刻t1和t2之间的状态转移是00→10;因为这个状态转移是由输入比特1产生的,所以译码器输出1作为第一位译码比特。由此可以看出,用实线表示输入比特0,虚线表示输入比特1,可以为幸存路径译码带来很大的便利。注意,只有当路径量度计算进行到网格图较深处时,才产生第一位译码比特。在典型的译码器实现中,这代表了大约是约束长度5倍的译码延迟。

在译码过程的每一步,到达每个状态的可能路径总有两条,通过比较路径量度舍弃其中一条。图8.26e给出了译码过程的下一步:在时刻t5到达各个状态的路径都有两条,其中一条被舍弃;图8.26f是时刻t5的幸存路径。注意,此例中尚不能对第二位输入数据比特做出判决,因为在时刻t2离开状态10的路径仍为两条。图8.26g中的时刻t6同样有路径合并,图8.26h是时刻t6的幸存路径,可见编码器输出的第二位译码比特是1,对应了时刻t2和t3之间的幸存路径。译码器在网格图上继续上述过程,通过不断舍弃路径直至仅剩一条,来对输入数据比特做出判决。

图8.26　幸存路径选择

网格图的删减(通过路径的合并)确保了路径数不会超过状态数。对于此例的情况,可证明在图8.26b、d、f、h中,每次删减后都只有4条路径。而对于未使用维特比算法的最大似然序列彻底比较法,其可能路径数(代表可能序列数)是序列长度的指数函数。对于分支字长为L的二进制码字序列共有2L种可能的序列。

5.译码器的实现

由图8.24的网格图可知,任意一个时间间隔内的状态转移可分组为2v-1个离散区间,每个区间描述4种可能的状态转移,其中,v=K-1,称为编码器记忆(encoder memory)。对K=3的例子,v=2,因此有2v-1=2个区间。这些区间如图8.27所示,其中a,b,c,d分别对应时刻ti+1的状态。在每个转移支路旁标有路径量度δxy,下标表示从状态x到状态y的转移,这些小区间以及与之相联系的逻辑单元描述了译码器的基本分组结构,逻辑单元用于更新状态量度{Γx},其中x指明特定的状态。

5.1　加-比较-选择计算

继续上面K=3的2区间例子,图8.28描绘了和区间1相应的逻辑单元,该逻辑单元进行的特殊计算,称为加-比较-选择(Add-Compare-Selet,ACS)。状态量度Γd的计算方法如下:将前一状态a的状态量度Γa和相应分支量度δaa′相加,将前一状态c的状态量度Γc和相应分支量度δca′相加,得到的两个可能路径量度作为新的状态量度Γ′a的候选项,送入图7.14的逻辑单元中进行比较,将其中似然性最大(距离最小)的一个作为状态a的新状态量度Γ′a存储,同时存储的还有状态a新的路径记录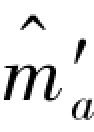,这里的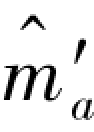是由幸存路径增添的状态信息路径记录。

图8.28中还有区间1中得到新状态量度Γ′b和新路径记录m^′b的ACS逻辑。其他区间中路径的ACS操作是类似的,译码器的输出是具有最小状态量度的最早比特。

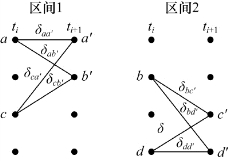
图8.27　译码器区间示例

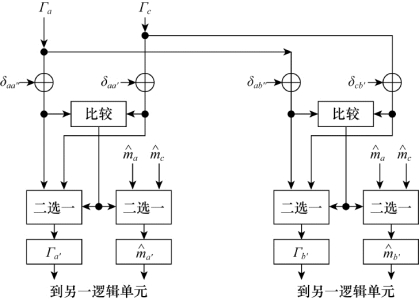
图8.28　对区间1完成加-比较-选择功能的逻辑单元

5.2　加-比较-选择在网格图上的表示

分析与描述维特比译码时相同的例子,信息序列m=11011,码字序列U=11 01 01 00 01,接收序列Z=11 01 01 10 01。图8.29描绘的译码器网格图与图8.24相似,各个分支上标注的路径量度,是接收的码元与编码器网格图上相应分支字之间的汉明距离。此外,在图8.29上还标注了每个状态x的值以及从时刻t2至时刻t6每个状态x的状态量度Γx。从时刻t4起,由于每个状态有两条到达路径,因此开始进行加-比较-选择操作(ACS)。例如在时刻t4,状态a的量度值有两个选择:一个是4,由时刻t3的状态量度值Γa=3加上分支量度δaa′=1得到;另一个是3,由时刻t3的状态量度值Γc=2加上分支量度δca′=1得到。ACS将具有最大似然性(最小距离)的路径量度作为新的状态量度;因此,在时刻t4状态a的新状态量度Γ′a=3。幸存路径用粗线表示,被舍弃的路径用细线表示。观察图8.29从左到右的状态量度,可以证明在每一时刻的各个状态量度值,是将幸存路径(粗线)上前一状态量度与前一路径量度相加而得到的。由网格图可知在网格图中的某个点上(经过4或5个约束长度时间间隔后)最早发送的编码比特已被译码。例如,观察图8.29的时刻t6,可以看出最小距离的状态量度值为1。从状态d开始,沿幸存路径追溯回t1时刻,可以看到译码信息与源信息是一样的,注意,为了方便起见,虚线和实现分别代表二进制数字1和0。

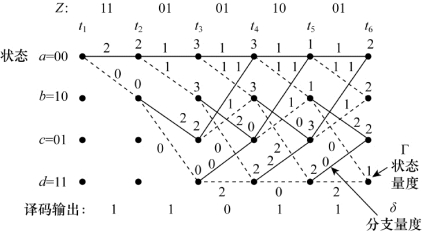
图8.29　维特比译码中的加-比较-选择计算

6.路径记忆与同步

维特比译码器的存储容量要求随约束长度K按指数增长。对于编码效率为1/n的编码,每一步译码后,译码器保留2K-1条路径。这些路径通常是在距离当前译码深度之前不远处分叉而得到的,所有这些路径是由公共支分叉到不同状态而生成的。因此,若译码器存储了这2K-1条路径的足够记录,可以看到所有路径的最早译码比特是一样的。因此,一个简单译码器的实现,包括固定数量的路径记录(fixed amount of path history),并且每次深入到网络的下一级时,在任意路径上输出最早的比特。所需路径存储量是

其中,h是每个状态的信息比特记录长度。一种改进算法是将最大似然路径上的最早比特代替任意路径上的最早比特作为译码器的输出,从而最小化h。可以证明,当h的值为编码约束长度的4或5倍时,足以获得接近最佳的译码器的性能。存储容量要求u是维特比译码器实现的基本限制,商业上生产的译码器受到约束长度K=10的限制。由式(8.65)可知,为了提高编码增益而增大约束长度,会带来存储容量要求按指数级的增加。

分支字的同步(branch word synchronization)是指对接收序列确定分支字的起始点的过程。这种同步不需要在发送的码元流中加入新的信息即可实现,因为未同步时接收数据会出现过大的差错概率;由此,实现该同步的种简单方法是,监督这个较大差错概率的伴随信息,如网格图上状态量度的增加速率或者幸存路径的合并速率;将这些被监督参数与一个门限值相比较,并相应地调整同步。