卷积码的关键特征是它的编码函数G(m),据此便可由输入序列m方便地计算输出序列U。下面分别介绍卷积编码器的一些常用描述方法,最常用的有连接图(connection pictorial)、连接矢量(connection vector)、连接多项式(connection polynomial)、状态图(state diagram)、树状图(tree diagram)以及网格图(trellis diagram)。

1.连接表示

下面以图8.17中的卷积编码器为例介绍卷积码编码器。该图表示一个约束长度K=3的(2,1)卷积编码器,模2加法器的数目为n=2,因此,编码效率k/n=1/2。在每个输入比特时间上,1位信息比特移入寄存器最左端的一级,同时将寄存器中原有比特均右移1级,接着便交替采样两个模2加法器(即先采样上面的加法器,再采样下面的加法器),得到的码元对就是与该输入比特相对应的分支字。对每一个输入信号比特都重复上述采样过程。加法器和寄存器各级间的不同连接将导致不同的代码性能。当然,连接方式不可以随意选择或者改变,而究竟如何选择能得到具有良好距离特性的连接方式,则是一个复杂的问题,尚未有通过的准则。不过,借助计算机搜索已经找到了所有约束长度小于20的好的编码。

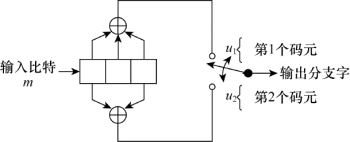
图8.17　卷积码编码器(编码效率1/2,K=3)

与分组码具有固定字长n不同,卷积码没有特定的分组结构。不过,人们常通过周期性的截断(periodic truncation)赋予其分组的结构。为了达到清空或冲洗编码移位寄存器数据比特的目的,需要在输入数据序列末尾附加若干个0比特。由于附加的0不包含任何信息,因而,有效编码效率(effective code rate)降至k/n以下。为了使编码效率尽可能接近k/n,截断周期一般取值较长。

描述编码器的一种方法是指定n个连接矢量集,每个矢量对应于一个模2加法器,每个矢量都是K维,表示该模2加法器和编码移位寄存器之间的连接。矢量中第i位上的1表示移位寄存器相应级与模2加法器的连接,若是0,则表示相应级与模2加法器之间无连接。以图8.17中编码器为例,可以写出代表上方连接的连接矢量g1和代表下方连接的连接矢量g2分别为

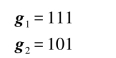
现在假设用图8.17的卷积码编码器对信息矢量m=101进行编码。如图8.18所示,3位信息比特在时刻t1,t2,t3依次输入,随后,(K-1)=2个0分别在时刻t4,t5输入以清空寄存器,从而确保信息的尾部也能完全移出寄存器。得到的输出序列是1110001011,其中,最左端的码元是最早发送的。整个输出序列(包括用于清空寄存器的2位0产生的码元)将用于译码。为了清空寄存器,共需K-1个冲洗比特,在t6时刻又输入一位0的目的,是为了说明在t5时已经完成了清空操作,即t6时刻已经可以输入新的信息。

1.1　编码器的冲激响应

现借助冲激响应(impulse response),即编码器对移入的单个“1”比特的响应,来分析编码器。当一位1通过图8.17中的寄存器时,寄存器的内容为

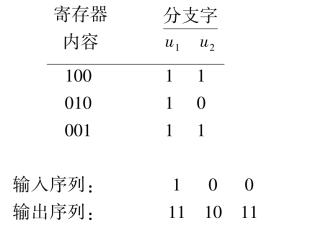
输入“1”所对应的输出序列就称为这个编码器的响应。输入序列m=101对应的输出可按如下方式线性叠加(linear addition)时移输入“脉冲”而得到:

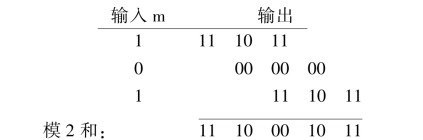
这里得到的输出序列和图8.18中的相同,可见卷积码和线性分组码都是线性码。由于可以通过将按时间移位的脉冲进行线性叠加,或者将输入序列和编码器的脉冲响应相卷积,来产生输出编码,因此这种编码器称为卷积码编码器(convolutional encoder)。卷积码编码器的特性常用无穷阶生成矩阵来描述。

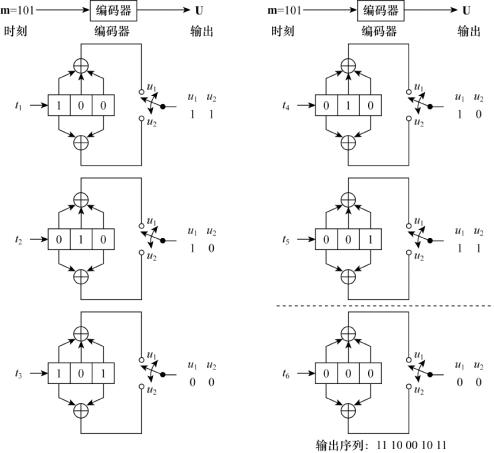
图8.18　编码效率为1/2,约束长度为3的卷积码编码器进行信息序列编码示例

注意,上例中输入3比特序列,输出10比特序列,有效编码效率为k/n=3/10,而根据每个输入信息比特对应两个输出信道比特的原理,期望的编码效率是1/2,两者差距较大。产生这个差异的原因是,为了将所有信息比特都移出寄存器而引入不含有效信息的比特0。输出的所有信道比特都将用于译码过程。如果信息序列较长,如300比特,那么相应的输出码字序列将是604比特,其编码效率300/604已经十分接近1/2。

1.2　多项式描述

用反馈移位寄存器实现循环码时所使用的生成多项式(generator polynomial),有时类似的过程也可以用于描述卷积码编码器的连接。应用n个生成多项式描述编码的移位寄存器与模2加法器的连接方式,n个生成多项式分别对应n个模2加法器,每个生成多项式不超过K-1阶。这种描述方法与连接矢量描述方法十分相似。这些K-1阶生成多项式中各项的系数为1或0,取决于移位寄存器和模2加法器之间的连接是否存在。仍以图8.17中的编码器为例,用生成多项式g1(X)代表上方连接,g2(X)代表下方连接,则有

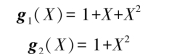
多项式中的最低阶项对应于寄存器的输入级。输出序列根据如下方式求得

先将信息矢量m=101表示成多项式形式——m(X)=1+X2。仍假设在信息序列后附加0以清空寄存器,该输入信息序列m经过图8.17所示编码器编码生成的输出多项式U(X),或输出序列U计算如下:

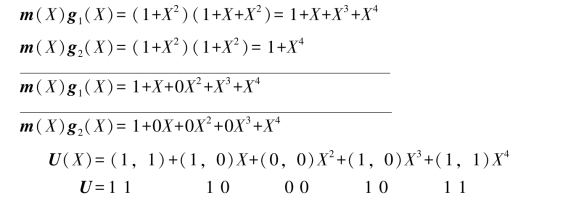
此例中引入另一种分析方法,即将卷积码编码器看作一组循环码移位寄存器,用描述循环码时引入的生成多项式来表示编码器,得到的输出序列与图8.18结果及前一节冲激响应方法的结果均一致。

2.状态描述和状态图(www.daowen.com)

卷积码编码器属于一类称之为有限状态机(finite-state machine)的器件,此通用名称用于表示对过去的信号具有记忆性的一类设备。“有限”表明状态机只有有限个不同的状态。那么,有限状态机的状态究竟指什么呢?就通常意义而言,状态可以用设备的当前输入和最少的信息数量,来预测设备的输出。状态提供了有关过去序列过程及一组将来可能输出序列的限制,下一状态总是受到前一状态的限制。以编码效率为1/n的卷积码编码器为例,状态就用最右端的K-1级寄存器内容来表示(见图8.17)。了解当前状态以及下一个输入,是确定下一输出的充要条件。将编码器在时刻ti的状态定义为Xi=mi-1,mi-2,…,mi-K+1。分支字Ui由状态Xi和当前输入比特mi完全确定,由此,状态Xi代表了编码器的过去信息,用以确定编码器的输出。编码器的状态是马尔可夫(Markov)的。只要编码器处于状态Xi+1的概率仅取决于最近的状态Xi,用公式表示为P(Xi+1/Xi,Xi-1,…,X0)=P(Xi+1/Xi)。

表示简单编码器的一种方法是状态图,图8.19就是对图8.17中编码器的状态图描述。该图方框内的状态表示寄存器最右端K-1级的可能内容,状态间的路径表示由此状态转移时的输出分支字。寄存器的状态表示为a=00,b=10,c=01,d=11,图8.19表示了图8.17编码器的所有可能状态转移。对于两种可能的输入比特,从每个状态出发只有两种转移,状态转移时的输出分支字标注在相应转移路径旁。图中,实线表示输入比特为0的路径,虚线表示输入比特为1的路径。注意,状态间的转移不是任意的,由于每次移入1个信息比特,故寄存器在每个比特时间上只有两种可能的状态转移。例如,如果编码器的当前状态是00,下一状态仅有两种可能,00或10。

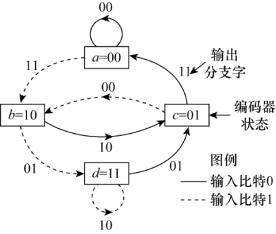
图8.19　编码器状态图(编码效率为1/2,K=3)

【例8.11】卷积编码

假定图8.17编码器的输入信息序列m=11011,并附加K-1=2个0以清空寄存器,假设寄存器初始状态是全0,求对应的状态变化及输出码字序列U。

解:

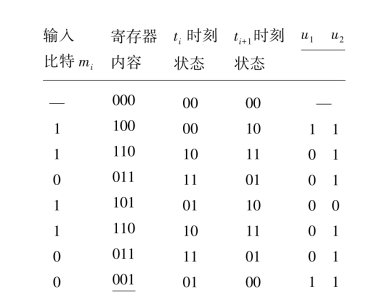
对上面划横线的001而言,前面的00表示为状态ti-1,后面的01表示为状态ti。则输出序列为:U=11 01 01 00 01 01 11

【例8.12】卷积编码

例8.11中寄存器的初始内容是全0,这相当于信息序列m前输入了两个0(编码是当前比特和前K-1比特的函数)。现在假设在信息序列m之前输入了两位l,证明信息序列m=11011对应的码字序列U与例8.11中的不同。

解:记号“×”表示“未知”

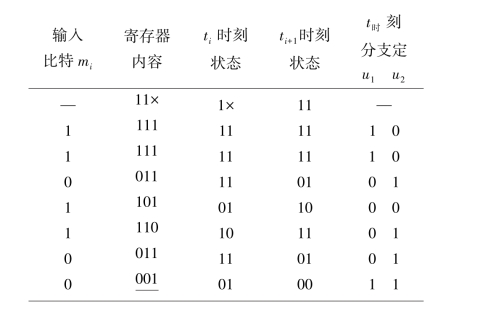
对上面划横线的001而言,前面的00表示为状态ti+1,后面的01表示为状态ti。则输出序列:　U=10 10 01 00 01 01 11

比较例8.11和例8.12可见,输出序列U的每个分支字不仅取决于相应输入比特,还取决于前K-1比特。

3.树图

虽然状态图完全地描述了编码器的特性,但由于没有表示时间过程,所以采用状态图跟踪编码器的状态转移很不方便。树状图在状态图的基础上增加了时间尺度。图8.17中所示卷积码编码器的树状图如图8.20所示,每个相继输入信息比特的编码过程可表述为从左向右经过树状图,每条树枝代表一个输出分支字。寻找码字序列的分支准则如下:如果输入比特是0,则向上方右移一个支路得到相应分支字;如果输入比特是1,则向下方右移一个支路得到相应分支字。假设编码器初始状态是全0,过程图显示如果第一位输入0,则输出分支字是00,如果第一位输入1,则输出分支字11。类似地,如果第一位输入1,第二位输入0,则第二个输出分支字就是10;如果第一位输入1,第二位输入1,则第二个输出分支字就是01。按照该准则在图8.20上用粗线表示出了输入序列11011在树状图上经过的路径。此路径对应于输出序列1101010001。

树状图上增加的时间尺度(与状态图相比)使我们可以动态地描述输入序列的编码过程,不过,用树状图描述编码过程也存在一个问题,即树状图的支路数按2L增加,L是序列中分支字的数目。树状图的规模增长很快,因此只适于L较小的情况。

4.网格图

观察图8.20中的树状图可知,在上例中,树状图从t4时刻,即经过第三条支路后开始重复自身结构(一般地,约束长度为K的树状图经过K次分支后开始重复自身结构)。采用移位寄存器的4种可能状态来标注图8.20中树的各个节点:a=00,b=01,c=10,d=11。树结构的第一次分支在时刻t1,产生一对节点,记为a,b;在后继的各个分支处,节点数翻倍。第二次分支在时刻t2,生成4个节点,记为a,b,c,d;第三次分支后,共有8个节点:两个a,两个b,两个c,两个d。通过观察可知,从处于同一状态的两个节点发出的所有支路产生相同的分支字序列,由此可知,树的上半部分和下半部分一致。分析图8.17中的编码器就可以对这一现象做出解释:当第4位信息比特从左端进入编码器时,输入的第1位信息比特已经从寄存器右端移出,不再影响输出分支字,因此,输入序列100xy…和000xy…(最左端的数据比特最先输入)在经过(K=3)次分支后产生相同的分支字。这一现象意味着,在同一时刻ti,具有相同状态的两个节点的后继分支将没有任何差别,因此,这两个节点可以合并。如果将图8.20的树状结构做这样的合并,则得到另一种图,称为网络图(trellis diagram)。网格图利用了结构上的重复性,用它来描述编码器比树状图更加方便。图8.17卷积码编码器的网格图如图8.21所示。

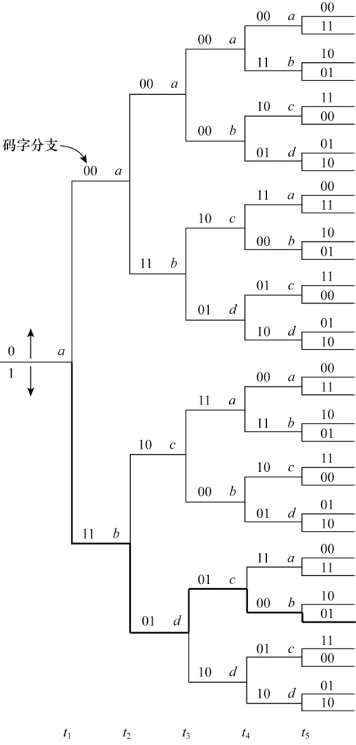
图8.20　编码器的树状图描述(编码效率为1/2,K=3)

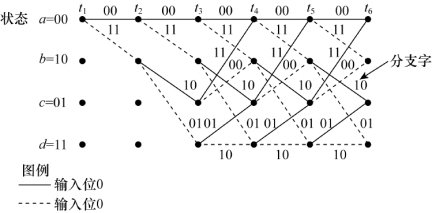
图8.21　编码器网格图(编码效率为1/2,K=3)

在画网格图时采用与画树状图时相同的规定,即实线表示输入一比特0时产生的输出,虚线表示输入一比特1时产生的输出。网格图的节点代表了编码器的状态:第一行节点对应于状态a=00,后继各行节点分别对应于状态b=01,c=10,d=11。在每个时间单元内,网格图用2K-1个节点表示2K-1个可能的编码器的状态。此例中的网格图在深度为3时(即t4时刻)得到固定的周期结构。一般情况下,固定的周期结构在深度为K时得到,自此以后,每一状态可以由前面两个状态中的任意一个输入;而且每一状态都有两种可能的状态转移,分别对应于输入比特0和输入比特1。图8.21中状态转移时的输出分支字标注在网格图分支上。

利用完整网格图的某个时间段内的信息就可以完全确定编码,这里画出多个时间段是为了把码元序列看成时间的函数。这里,卷积编码器的状态用编码寄存器最右端的K-1级的内容表示,也有著者用编码寄存器最左端的K-1级的内容表示。从如下所述的观点来看,这两种表示方法都正确。每一次状态转移都包括一个初始状态和一个结束状态,最右端的K-1级表示了当前输入对应的初始状态,此时,当前输入在最左端的1级中(假设编码器的编码效率为1/n);而最左端的K-1级表示这次状态转移的结束状态。输出的码元序列由占用N个时间段的N个分支组成(对应于输入的N个比特),由始至终的N+1个时刻都对应着特定的状态。由此,我们在时刻t1,t2,…,tN输入信息比特,而分析时刻t1,t2,…,tN+1的状态。这里规定,当前比特在寄存器的最左端级中(不在进入该级的信号线上),寄存器最右端的K-1级初始状态为全0,该时刻称为初始时刻(start time),标记为t1。将最后一次状态转移的末时刻称为结束时刻(terminating time),标记为tN+1。