码字在传输中可能受到噪声干扰。因此,接收到的矢量有可能并不是发送的矢量。假设传输的码字具有多项式表达形式U(X),而接收到的矢量其多项式表征为Z(X),因为U(X)是一个码字多项式,它必是生成多项式g(X)与某个多项式的乘积,即

而Z(X)是U(X)受到干扰后的形式,可以写为

其中,e(X)是错误图样的多样式。译码器检验Z(X)是否为一个码字多项式,即它除以g(X)后,余项是否为0。这是通过计算接收多项式的伴随式(syndrome)实现的。伴随式S(X)等于Z(X)除以g(X)的余项,即

其中,S(X)是一个n-k-1或更低阶的多项式。这样,伴随式是一个(n-k)元组。由式(8.53)到式(8.55),可得(www.daowen.com)

比较式(8.55)和式(8.56),可以发现伴随式S(X)作为Z(X)模g(X)的余式,恰好等于e(X)模g(X)的余式。这样接收矢量多项式Z(X)的伴随式就包含了纠正错误图样的信息。伴随式的计算是通过除法电路实现的,几乎与发送器所使用的编码电路相同。图8.14是一个用(n-k)级移位寄存器计算伴随式的例子,这里码字矢量的生成同例8.10。开关1开始是闭合的,而开关2打开。开始时所有存储单元初始化为0,接收矢量移入寄存器的输入端。当整个接收矢量进入移位寄存器后,寄存器的内容就是伴随式。然后,打开开关1,合上开关2,这样就把伴随式移除寄存器。译码器的操作步骤如下:

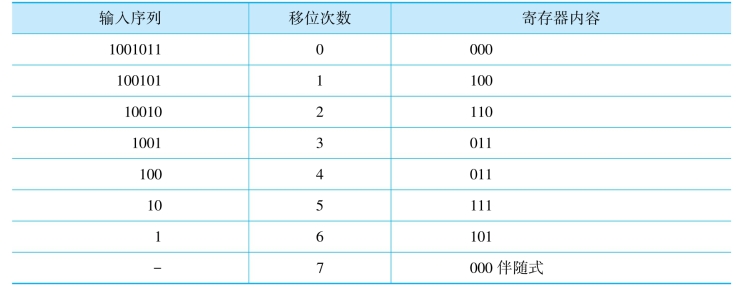
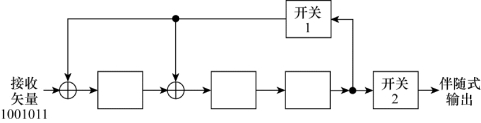
图8.14　(n-k)级移位寄存器计算伴随式的例子

如果伴随式是全0矢量,就认为接收到的矢量是正确的码字。如果伴随式是非0矢量,则接收的矢量就受到了干扰,即检测到了错误的发生;这些错误可以通过将错误矢量(由伴随式指明)加于接收矢量得到纠正。这种译码方法对简单的码字是十分有效的。更复杂的码字则需要使用代数技巧来获得实用的译码器。