对于前一小节的(8,2)码系统,(k×n)=(2×8)生成矩阵可以写为

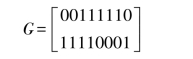
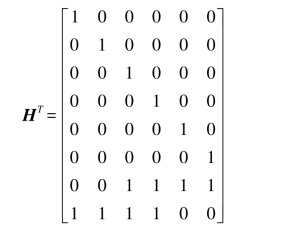
从计算伴随式开始进行译码,这可以认为是了解错误的“症状”。对于(n,k)码,一个(n-k)比特的伴随式S是n比特的接收矢量r和一个(n-k)×n的监督矩阵H转置的乘积。这里,H的行正交于G的行,即GHT=0。对于这个(8,2)码的例子,S是一个6比特矢量,而H是一个6×8的矩阵,即

对于每个错误图样,可以通过式(6.37)计算伴随式,即

其中,Si是2n-k=64个伴随式之一,ei是标准阵列中64个陪集首(错误图样)之一。图8.9以表格形式列出了标准阵列和(8,2)码的所有64个伴随式。伴随式的集合由式(8.26)计算而得。标准阵列的每一行(陪集)的元素都有相同的伴随式。对受到干扰的码字的纠正是通过计算它的伴随式找出其对应的错误图样。随后错误图样和受到干扰的码字模2加,生成正确的输出。纠错能力和检错能力是可以权衡的,只要距离关系dmin=α+β+1成立;其中,α代表了需要纠正的错误比特数,β代表了需要检测的错误比特数,β≥α。对于(8,2)码的例子,可以采用的权衡选择如下:

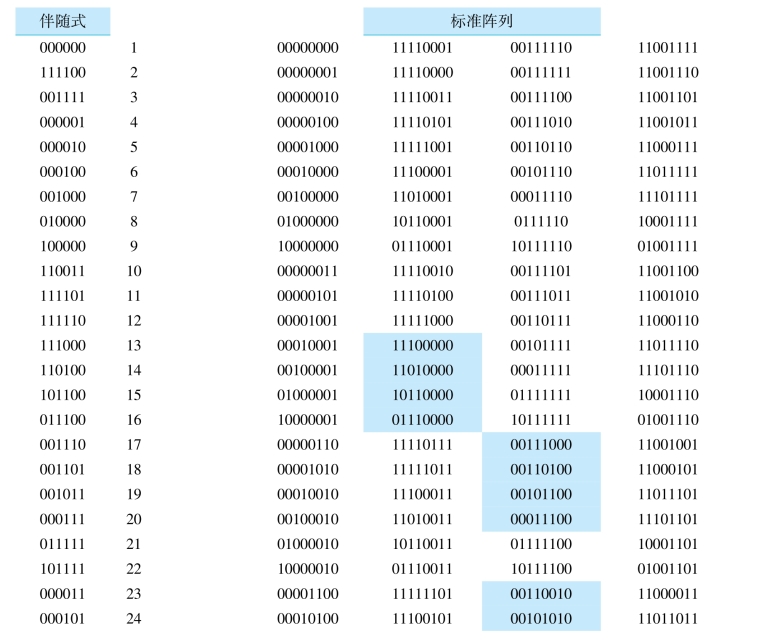
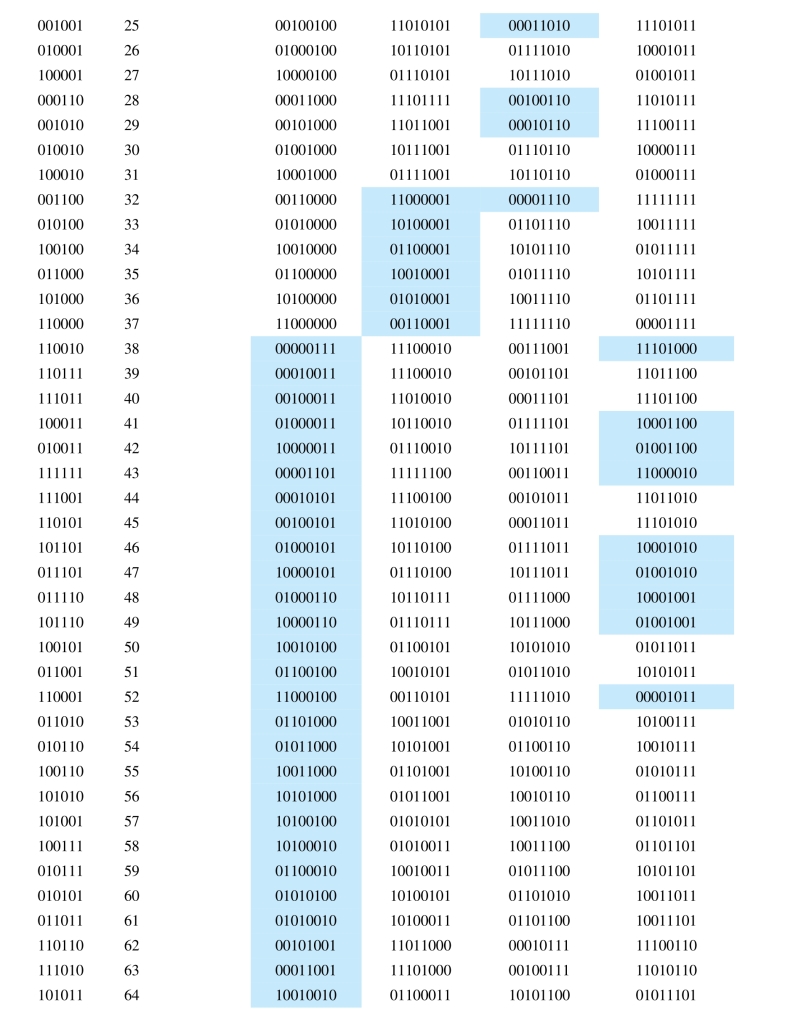
图8.9　标准阵列和(8,2)码的所有64个伴随式(www.daowen.com)

该表显示了(8,2)码可以只用来实现纠错,这意味着它首先检测到多达β=2个错误,然后纠正它们。如果减少纠错能力使码只能纠一个错误,那么,检错能力上升到可以检测到β=3个错误。最后,如果完全放弃纠错能力,那么译码器可以设计成能检测到所有β=4个错误。在只检错的情况下,电路十分简单。计算伴随式,当只要有一个伴随式非零时,即检测出有错。

对于纠正单个错误,译码器可以通过门电路实现,类似于图8.6的电路,接收矢量进入两个位置。在图的上半部分,接收矢量进入异或门,产生伴随式。对于所有给定的接收矢量,伴随式可以通过式(8.24)获得

根据(8,2)码的HT的值,接收矢量和异或门之间的连线电路类似于图8.6中的那一个,连接后可以得到

组成伴随式Si(i=1,…,64)的每一个数字sj(j=1,…,6)按下列方式与输入端接收的码字矢量相关联:

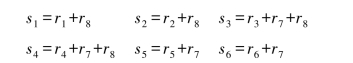
要实现类似于图8.6中的(8,2)码的译码器电路,需要将8个接收数字与上面描述的6个模2加法器产生的伴随式数字联系起来。相应地,需要对此图做额外的修改。

如果译码器只要求纠正单个错误,即α=1且β=3,那么,这等于在图8.9的陪集9下面画一条线,只有当与单个错误相对应的8个伴随式出现时才进行纠错。然后译码电路(与图8.6类似)将伴随式变换为它对应的错误图样。随后,错误图样与可能受到干扰的接收矢量模2相加,产生正确的结果。另外需要一些附加的门在产生了非零伴随式,但是并没有设计其对应的纠正时作检测使用。对于纠正单错的情况,这种事件发生于任何一个序号在10到64之间的伴随式。其结果用来指示检测到了错误。

如果译码器用于纠正所有的单错和双错,这意味着β=2的错误被检测并被纠正,这等于在图8.9标准阵列的陪集37下画一条线。尽管这个(8,2)码有能力检测到一些三错的组合,这时对应于38到64的陪集首,但我们通常把译码器设计成界限距离译码器,这意味着它能纠正所有少于或等于t个错误组合,却不能纠正多于t个错误的组合。没有使用的纠错能力被用来增强一些检测能力。与前面的一样,译码器可以类似于图8.6,用门电路实现。