可以将标准阵列想象成一个有组织的管理工具,一个被填满的小屋,它装着所有的n元组空间中的2n个项——没有遗漏,也没有重复。直觉上看,这个工具的好处局限于小的分组码,因为码字长度大于n=20时,空间中将有数以百万计的n元组。不过,即使对于较大的码本,标准阵列也可以将一些重要性能问题,例如在纠错和检错间权衡的可能性以及纠错能力的界限等,进行可视化处理。一种称为汉明界限(Hamming bound)的界限表述如下:

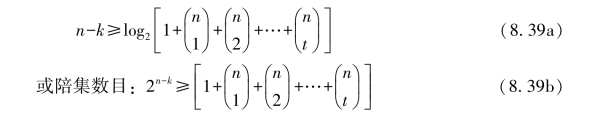
其中,表示n位中有j比特出错的可能形式的数目。注意,式(8.39)中方括号内各项之和得出了标准阵中所需的、纠正所有t位错误线性组合的最小行数。不等式给出了监督比特的数目n-k(或2n-k个陪集的数目)的下界是码的t位纠错能力的函数。类似地,不等式可以描述成t位纠错能力上界是n-k个监督比特(或2n-k个陪集)的函数。对于任意一个能提供t位纠错能力的(n,k)线性分组码,满足汉明界限是一个必要条件。

为了说明标准阵列是怎样提供这个界限的视图的,不妨选择(127,106)BCH码作为一个例子。阵列包含了空间中的所有2n=2127≈1.70×1038个n元组。阵列最上面的一行包含了2k=2106≈8.11×1031个码字;因此,这就是阵列的列数。最左边的一列包含了2n-k=221=2097152个陪集首,因此,这就是阵列的行数。尽管n元组和码字的数目巨大,但我们并不关心每一个单独的条目,主要关心的是陪集的数目;共有2097152个陪集,因此,这种码最多只能纠正2097152个错误图样。另外,它显示了陪集的数目是怎样决定码的t位纠错能力的上界的。(www.daowen.com)

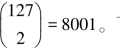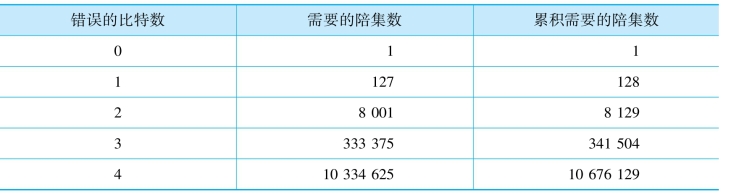
由于每个码字都包含127比特,因此有127种方式形成单个错误。可以计算出构成两个错误有多少种情况,即下面继续分析出3个错误的情况,因为到目前为止,总共2097151个可纠正的错误图样中,只使用了很少一部分。一共有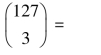333375种方式可以组成3个错误。表8.4中列出了这些计算结果,说明全0错误图样要求第一个陪集的出现,其后是单错、双错和3个错误。表中同样说明了每种错误类型所需要的陪集数和到该种错误类型为止所需要的累积的陪集数。从该表中可以看出。(127,106)码可以纠正所有的单错、双错、三错图样,而这些只需要所有可用的2 097 152个陪集中的341 504种。没有使用的1 755 648行表明了更多位纠错的可能性。实际上,可以试图把所有的4错图样映射到阵列中,但是由表8.4可以看出,这是不可能的,因为正如表8.4中最后一行显示的那样,阵列中剩下的陪集数比纠正4错图样所需的累积陪集数小得多。因此,对于这个(127,106)的例子,该码的汉明界限保证了可以纠正小于等于3个错误的所有图样。

表8.4　(127,106)码的纠错界限