图8.8是前面的例子中8个码字的视图。码字组由式(8.16)中三个独立的6元组经线性组合而成。这些码字构成了一个三维子空间。此图表示了一个由8个码字完全占据的(大黑圆圈)的子空间;子空间的坐标特意被画出以强调其并非正交。尽管并没有精确的方法来画出或构建这样的模型,但是图8.8仍试图说明一个包含64个6元组的整个空间。球形的层或者壳围绕着每个码字。每一个不相交的内层与它对应的码字间的汉明距离为1,每一个外层与它对应的码明距离为2。此例中没有使用更大的距离。对于每一个码字,画出的两层被受到干扰的码字占据。每个内层都有6个这样的点,(总共有48个点),代表了对应于各个码字的6个可能的1比特干扰错误矢量。这些1比特干扰的码字仅与一个码字呈现最佳关联,从这个意义上说,它们可以互相区分,因此可以被纠正。正如从图8.5中看到的标准阵列,只有一个2比特错误图样可以纠正。总共有种不同的2比特错误图样可以加于每个码字上,但其中只有1个可以被纠正(在我们的例子中是010001错误图样)。其他的14种2比特错误图样产生的矢量,难以被唯一地鉴别为单一的码字;这些不可纠正的错误图样产生的矢量,与两个或更多码字受到错误干扰的矢量相同。在图中,所有可纠正的(56)1比特或2比特错误干扰的码字都被画成小黑圈,受到干扰而不能纠正的码字被画成白圈。

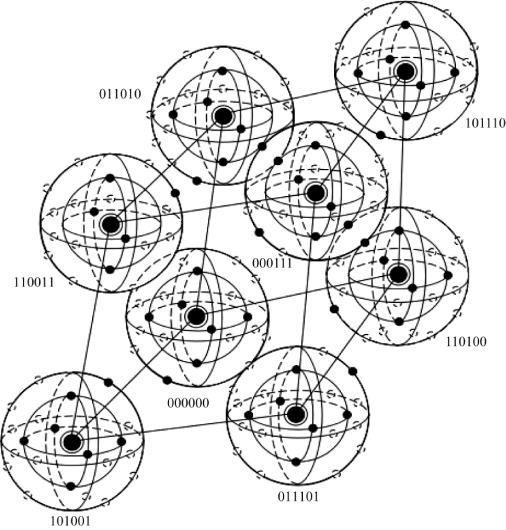
图8.8　6元组空间中的8个码字示例(www.daowen.com)

如图8.8所示的一类码称为完备码(perfect code),图中描述了这种码的性质。如果一个t比特纠错码的标准阵列包括了所有t位或更少位错误的错误图样,且不含有其他的陪集首(没有剩余的纠错能力),它就称为完备码。根据图8.8,一个t位纠错的完备码,采用最大似然译码时,能够纠正所有与原码字的汉明距离为t或小于t的干扰码字,而不能纠正与原码字距离大于t的码字。

图8.8对于理解寻找良好性能编码的目标也是十分有用的。我们希望空间中存在尽可能多的码字(有效利用增加的冗余度),但同时也希望码字间的距离尽可能大。显然,这些目标是互相矛盾的。