译码器的任务是,在接收到矢量r后,估计出传输的码字Ui。最佳的译码器策略可以用最大似然(maximum likelihood)算法表示如下:如果

则判决为Ui。因为在二进制对称信道(BSC)中,r是Ui的可能性,与r到Ui之间的距离成反比,可以写为:如果

则判决为Ui。换句话说,译码器计算r与每一个可能的传输码字Uj的距离并选出最可能的满足下式的Ui:

其中,M=2k是码字集合的大小。如果最小距离不是唯一的,那么任意选择最小距离码字中的一个。

在图8.7中,两个码字U和V的距离表现为一条由汉明距离作刻度的数字线。每一个黑点代表一个受到干扰的码字。图8.7(a)中接收矢量r1,它与U的距离为1,而与V的距离为4。采用最大似然准则的纠错译码器,在收到r1时将选择U。如果r1是传输矢量U被1比特干扰的结果,那么纠错是正确的。但是如果r1是传输矢量V受到4比特干扰的结果,那么译码就是错误的。类似地,U在传输中出2个错的结果是r2,它与U的距离为2而与V的距离为3,如图8.7(b)所示,这里,译码器也将在收到r2时选择U。如果U在传输时发生3个错误,则将导致接收到r3,r3与U的距离为3而与V的距离为2,如图8.7(c)中所示,这样译码器将在收到r3时选择V,从而在译码时出错。从图8.7可以很清楚地看出,如果任务是检错而不用纠错,一个受干扰的码字(用黑点表示,代表1比特、2比特、3比特、4比特错误)可以被检测到。不过,出5比特错时,在传U的时候会接收到V;这样的差错是不可检测的。

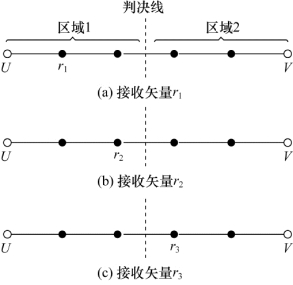
图8.7　纠错和检错能力

从图8.7可以看出,码的检错和纠错能力是由码字间的最小距离决定的。图中的判决线在译码和解调过程中起相同的作用,即定义判决区间。在图8.7的例子中,如果r落入区域1就选择U,落入区域2就选择V,这种判决标准表明,对于这样的码(dmin=5)可以纠正2比特错误。一般说来,码的纠错能力t是由每个码字确保的最大纠错个数来定义的,即

其中,[x]代表不超过x的最大整数。通常,一个可以纠正所有t个或少于t个错误的序列的编码,也可以纠正一些特定的t+1个错误的序列,这可以从图8.5中看出。在这个例子中dmin=3,这样由式(8.33)看到,所有t=1比特的错误图样都是可以纠正的。同样,一个t+1即2比特的错误图样也是可纠正的。一般说米,一个t比特纠错(n,k)线性码有能力纠正总共2n-k个错误图样。如果一个比特纠错分组码被严格地用来在一个转移错误概率为p的二进制对称信道(BSC)中纠错,消息错误的概率PM即译码器做出错误译码,N位分组出错的概率,可以得出上界:

只有当译码器能够纠正所有小于等t的错误组合,而不能纠正多于t个错误组合的时候,这个界限才取等号。这种译码器称为界限距离译码器(bounded distance decoder)。译码的误比特率PB取决于特定的码本和译码器,它可以通过下式近似表示:

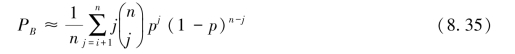
一个分组码需要在纠错之前先检错,或者它可能只用于检错。从图8.7中可以看出,所有标了黑点的接收矢量(受到干扰的码字)都可以判为有错。这样,检错的能力用dmin的形式定义就是

(www.daowen.com)

最小码间距离为dmin的分组码,可以保证所有具有dmin-1或更少错误的图样能够检测到。这样的码也能检测出大部分有dmin或更多错误的图样。实际上,一个(n,k)码有能力检测2n-2k个长度为n的错误图样。其原因如下:对于2n个可能的n元组空间,共有2n-1种可能的错误图样。即便是一个有效的码字也可能是潜在的错误图样。这样2k-1个错误图样就与2k-1个非零码字相同,如果这2k-1个错误图样中任何一个出现,它将传输的码字Ui转变为另一个码字Uj。这样,Uj将被接收而它的伴随式是0,译码器接收Uj作为传输的码字,于是做了错误的译码。因此,有2k-1种不能检测的错误图样。如果错误图样不同于2k个码字中的任一个,那么,伴随式检测对于接收矢量会产生一个非0伴随式,从而检出错误。因此,一共有恰好2n-2k种可检测的错误图样。对于大的n,有2n＜2k,只有很小一部分的错误图样不能检测。

1.码字重量分布

令Aj为(n,k)线性码中重量为j的码字的数目,那么A0,A1,…,An称为码的重量分布(weight distribution)。如果在二进制对称信道上编码只用于错误检测,则译码器不能检测到错误的概率可以通过码的重量分布求出:

其中,p是二进制对称信道的传输概率。如果码的最小距离是dmin,则从A1到Admin-1的值都是0。

【例8.6】检错码中出现不能检测错误的概率

考虑前面给出的(6,3)码,只用于检错。计算信道是二进制对称信道且转移概率为10-2时,一个错误不能被检测到的概率。

解:该码的重量分布为A0=1,A1=A2=0,A3=4,A4=3,A5=0,A6=0。因此,根据式(8.37),可得

对于p=10-2,一个错误不能检测出的概率是3.9×10-6。

2.同时纠错和检错

可以将由式(8.33)给出的最大可保证的纠错能力(t)降低,从而同时能够检测一些错误。如果最小码距满足下述条件,则这种码可以同时纠正α个错,并检测β个错(其中β≥α):

当有t个或更少的错误出现时,码有能力检测并纠正之。当多于t但少于e+1个错误出现[其中,e当由式(8.36)定义]时,码有能力检测出错码的存在,但只能纠正它们的一个子集。举例来说,一个dmin=7的码可以采用以下的任一种方式同时检错和纠错:

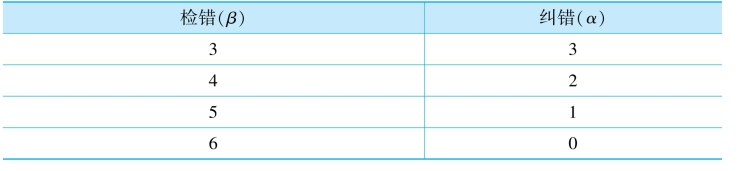
注意,纠错意味着先检错。对于上面的例子,当有3个错时,它们都能被检测出来并被纠正。当有5个错时,它们都能被检测,但只有其中的子集(1个)可被纠正。