在码比较短的情况下,如同在前面一节描述的(6,3)码,译码器可以用简单的电路实现。考虑译码器必须采取的步骤:(1)计算伴随式;(2)找出错误图样;(3)对错误图样和接收到的矢量执行模2加运算(除去错误)。在例8.5中,从一个被干扰的矢量开始,可以看到以上这些步骤如何产生正确的码字。现在考虑图8.6中的电路由异或门和门组成,它可以与(6,3)码的单个错误图样产生相同的结果。根据表8.3和式(8.28),可以根据接收到的码字为每个伴随式写出表达式

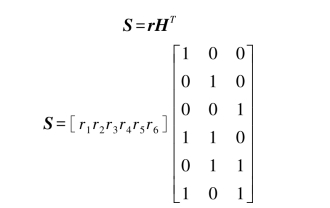
和

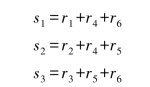
下面用这些伴随式构成图8.6中的电路。异或门进行的是模2算数加的操作,因此使用相同的符号。进入与门的连线结尾的小圆圈代表信号的逻辑取反。

受到干扰的信号同时进入译码器的两个位置。在电路上端,计算伴随式,在电路的下端,伴随式变为它对应的错误图样。通过把错误图样加到接收矢量以产生正确的码字,这样就消除了错误。

(www.daowen.com)

图8.6　(6,3)译码器的实现

注意,为了讲解方便,图8.5只强调了代数译码步骤——伴随式的计算、错误图样和正确的结果。实际情况是,一个(n,k)码通常设置为系统码,译码器不需要输出整个码字;它的输出只要仅仅包含数据比特。因此,图8.5通过删除带阴影的门得到简化。对于较长的码,这种实现非常复杂,更常使用的译码技术是通过采用串行方法而不是并行方法简化电路。同样需要强调的是,图8.5只能检测和纠正(6,3)码单个错误的图样。对两个错误图样的控制需要更多的电路。

码字、错误图样、接收矢量和伴随式分别用矢量U,e,r和S表示,为了简化起见,表示一个矢量所用的下标通常被省略,准确地说,这些矢量U,e,r,S,每一个都是一个集合,具有如下一般的形式:

考虑下标j和i在表8.2中(6,3)码的取值范围。对于码字Uj,下标j=1,…,2k表明有23=8个不同的码字,而下标i=1,…,n代表每一个码字由n=6比特组成。对于一个可纠正的错误图样ej,下标j=1,…,2n-k代表有23=8个陪集首(7个非零可纠正的错误图样),而下标i=1,…,n代表每一个错误图样由n=6比特组成。而对于接受矢量rj,下标j=1,…,2n代表有26=64个可能的n元组可能被接收到,而下标i=1,…,n代表每一个接收到的n元组有6比特。最后,对于伴随式Sj,下标j=1,…,2n-k代表有23=8个不同的伴随式矢量,而下标i=1,…,n-k代表每一个伴随式由n-k=3比特组成。在本章中,下标通常被省略去,而矢量Uj,ej,rj和Sj分别记为U,e,r和S。