前面已经检测了单个错误,并说明无论是错误码字,还是导致其错误的错误图样,伴随式检验都能产生相同的伴随式。这样,不仅可以检测错误,而且可以同时纠正错误,因为可纠正的错误图样与伴随式之间呈现一一对应的关系。现在用一个矩阵表示所有可能的2n个n元组的接收矢量,这个矩阵称为标准阵(standard array),第一行以全0码字开始,包括了所有码字,而第一列包括了所有可纠正的错误图样。回忆一下线性码的基本性质,即全0矢量必须是码字集的一个成员。每行称为一个陪集(coset),由第一列的错误图样(称为陪集首)及其干扰的码字组成。(n,k)码的标准阵形式如下:

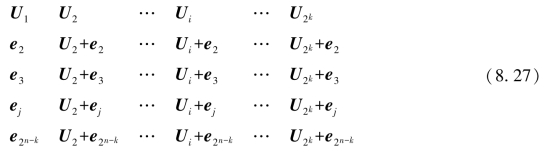
注意,码字U1(全0码字)起两个作用:既是其中一个码字,也是错误图样e1,代表没有错误,即r=U。该矩阵包括了Vn空间中所有的2n个n元组。每个n元组只出现在一个位置(没有一个缺少,也没有一个重复)。每个陪集包含2k个n元组,因此共有(2n/2k)=2n-k个陪集。

译码机制要求将每个有错的矢量用与此矢量同列的最顶端有效码字代替。假设一个码字Ui(i=1,2,…,2k)通过一个噪声信道,接收矢量为Ui+ej,如果错误图样ej是一个陪集首,其中j=1,…,2n-k,则接收矢量将被正确译码为码字Ui。如果错误图样不是一个陪集首(coset leader),那么将会导致译码错误。

1.陪集的伴随式

如果ej是第j个陪集首或错误图样,那么Ui+ej是此陪集中的一个n元组。这个n元组的伴随式可以写为

陪集是“具有相同特征的数字集”。对于任意给定的行(陪集),成员之间存在什么共同点?从式(8.28)可以清楚地看到,陪集中的每一个元素具有相同的伴随式(syndrome)。编码时每个陪集的伴随式是不同的。伴随式用于估计错误图样。

2.纠错译码

纠错译码的过程如下:

(1)计算r的伴随式S=rHT。

(2)定位错误图样(陪集首)ej,它的伴随式与rHT相等。

(3)假设错误图样是由信道衰落引起的。

(4)错误接收的矢量或码字表示为U=r+ej。通过减去其中已识别出的错误来恢复正确的码字。

模2运算中,减运算与加运算相同。

3.错误图样的定位

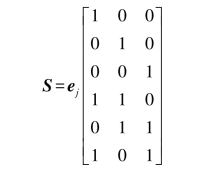
将26=64个6元组如图8.5所示排列成一个标准阵。有效码字是第一行的8个矢量,可纠正的错误图样是第一列的7个非零陪集首。注意,所有1比特错误图样都可以纠正。同时,除去所有1比特的错误图样,还有一些可纠正的错误,因为并没有用完所有64个6元组。还剩一个未分配的陪集首,因而还可以纠正一个附加的错误图样。可以灵活地将此错误图样定为010001。当且仅当信道引起的错误是其中一个陪集首时,译码才是正确的。

现在,通过计算ejHT来确定每个可纠正错误序列的伴随式,即

(www.daowen.com)

图8.5　(6,3)码的标准阵示例

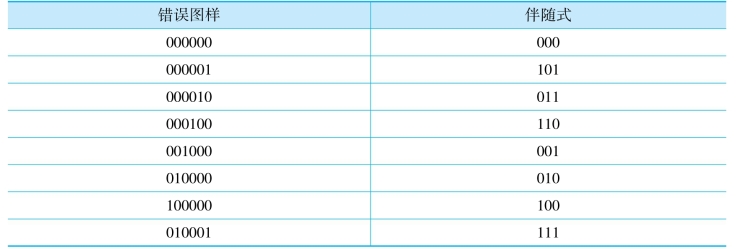
结果列于表8.3。由于表中的每个伴随式都是唯一的,译码器可以确定与e对应的错误图样。

表8.3　伴随式查询表

4.纠错举例

我们得到矢量r,并用S=rHT计算其伴随式。然后利用前面部分得到的查询表(表8.3),求出相应的错误图样。这个错误图样是对错误的一个估计,记为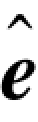。译码器然后将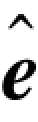加到r上得到一个估计的发送码字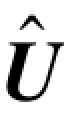

如果估计的错误图样与真实的错误图样相同,即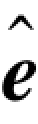=e,那么估计值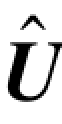等于发送码字U;如果错误估计不正确,则译码器得到的估计值不是发送的码字,这是一个无法检验的译码错误。

【例8.5】纠错

假设发送码字U=101110,接收矢量r=001110。根据表8.3的伴随式查询表,试说明译码器是如何纠错的。

解:r的伴随式计算如下:

利用表8.3,与此伴随式对应的错误图样估计为

正确的矢量估计为

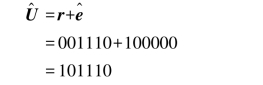
因为,此例中估计的错误图样就是实际的错误图样,所以由纠错过程得到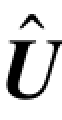=U。

注意,对于受干扰码字的译码,首先要检测,然后纠正一个错误,这一过程可以与医疗过程做个类比。病人(可能受到干扰的码字)进入医疗机构(译码器);检查的医生做了一个诊断(乘以HT),以找到症状(伴随式)。想象医生找到了病人X光照片上的特定点,一个有经验的医生会立即将症状与疾病肺结核病(错误图样)联系起来。而一个新手医生可能还要参阅一下医科手册(表8.3),将症状(伴随式)与病症(错误图样)联系起来。最后一步是提供合理的治疗来消除疾病,就像式(8.29)所看到的一样。在二进制编码与医疗的类比中,式(8.29)揭示了一种特殊的医学实践方法,即病人通过重新运用原来的疾病而获得治疗。