当k很大时,编码器查询表(table look-up)的实现比较复杂。对一个(127,92)码,有292个或5×1027个码矢量,如果编码过程由一个简单的查询表组成,容纳如此之多码字所需要的存储器的容量将是巨大的。幸运的是,可以按需随时产生码子而非存储码字来减少复杂性。

由于形成线性分组码的码字集是n维二进制矢量空间的一个k维子空间(k＜n),因而总能够找到一个n元组集合,它包含的矢量个数少于2k个,但可以用它产生子空间的2k个码字。产生的矢量集称为扩展子空间。用于扩展子空间的最小线性无关(linary independent)集称为子空间的基(basis),该集合中包含的矢量个数称为该子空间的维数。任意k个线性独立n元组V1,V2,…,Vk的一个线性组合,也即,2k个码字{U}中的任意一个都可以描述为

其中,mi=(0或1)是消息数字,i=1,…,k。

通常可以按如下方法定义一个生成矩阵(k×n):

码字矢量通常用行矢量描述。这样,k个消息比特的序列m表示为一个行矢量(1×k):

码字U是m与G的乘积,用矩阵形式表示为(www.daowen.com)

采用以下的规则实现矩阵的相乘C=AB:

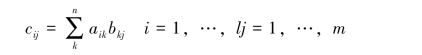
其中,A是l×n矩阵,B是n×m矩阵,结果C是l×m矩阵。对于前面介绍的例子,可以将生矩阵定义为

其中,V1,V2,V3是三个线性无关矢量(是8个码矢量的一个子集)。用它们可以产生所有的码矢量。注意,任意两个生成矢量的和不能够产生任何其他的生成矢量(与封闭性相反)。现根据式(8.16)的生成矩阵,表8.2中的第4个消息矢量110生成码字U4,即这样,对应于一个消息矢量的码矢量是矩阵G的行矢量的线性组合,既然这个码字完全由G确定,那么编码器只要存储G的k个行而非2k个矢量。对于此例,注意,用式(8.16)的3×6生成矩阵代替表8.2中8×6维原始码字矩阵,带来了系统复杂性的降低。