由于信源每秒钟产生的信源符号数与信道中每秒钟传送的信道符号数通常不一样,因此实际信息传输系统往往需要从单位时间来考虑,实现有效、可靠传输的条件由定理8.3给出。

定理8.3(联合信源信道编码定理)　离散无记忆信源S的熵值为H(S)(比特/信源符号),每秒钟输出1/Ts个信源符号;离散无记忆信道的信道容量为C(比特/信道符号),每秒钟输出1/Tc个信道符号。如果满足

或

则总可以找到信源和信道编码方法,使得信源输出信息能通过该信道传输后,平均错误概率PE任意小。

【例8.2】设一个二元对称信道,错误概率p=0.02,设该信道以2000二元符号/秒的速率传送消息,现有长度为15 000的独立等概的二元符号序列通过该信道传输,试回答实现该符号序列无差错传输的最短时间是多少?

解:二元对称信道的容量为

即每秒钟信道传送的信息量为

设实现该符号序列传输的时间是T秒,因信源熵为1比特/信源符号,符号序列长度为15 000,则信源每秒钟输出的信息量为15 000/T。根据联合信源信道编码定理,有

即T＞8.74s时,该符号序列可以无差错传输。

在实际通信系统设计中,为了做到既有效又可靠地传输信息,通常将通信系统的编码设计为信源编码和信道编码两部分。首先针对信源特性进行信源编码,然后针对信道特性设计信道编码。由于无失真信源编码和译码都是一一对应的变换,因此它不会带来任何的信息损失;而信道编码只要满足Ct＞Rt,就存在某种编码方法,使得平均错误概率PE任意小。因此满足式(8.16),分两步处理不会增加信息损失,它和一步编码处理方法同样有效。

下面通过一个例子来理解联合信源、信道编码定理。

【例8.3】设某二元无记忆信源

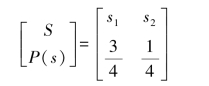
(1)如果信源每秒钟发出2.3个信源符号,将此信源的输出符号送入无噪信道中进行传输,而信道每秒钟只传送2个二元符号。通过适当编码,信源是否能够在此信道中进行无失真传输?试说明如何进行适当编码。

(2)如果信源每秒钟发出2.3个信源符号,送入二元对称信道中进行传输,而信道每秒钟传送25个二元符号。已知信道矩阵为

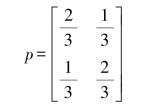
是否存在一种编码方法,使得信源输出信息能通过该信道传输后,平均错误概率PE任意小?

解:信源熵比特/信源符号

(1)二元无噪信道的最大信息传输率

(www.daowen.com)

而信道每秒钟传送2个符号,所以该信道的最大信息传输速率

如果信源每秒钟发送2.3个信源符号,则信源输出的信息速率

则

所以,通过适当编码,信源能够在此信道中进行无失真传输。如何进行编码呢?可以对N次扩展信源进行霍夫曼编码,然后再送入信道。当N=2时,编码结果如表8.1所示。

表8.1　N=2时的编码结果

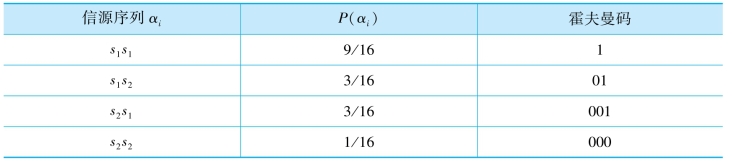
当N=2时,单个符号的平均码长

所以,二次扩展编码后,送入信道的传输速率为

信源编码得到的二元码符号进入信道,即信道符号就是二元码符号,由题意可知,信道每秒钟可以传送两个符号。因为1.94＜2,此时就可以在信道中进行无失真传输。

(2)该二元对称信道的信道容量

而信道每秒钟传送25个符号,所以该信道的最大信息传输速率

如果信源每秒钟发送2.3个信源符号,则信源输出的信息速率

则

由联合无失真信源信道编码定理可知:理论上存在一种编码方法,使得信源输出信息能通过该信道传输后,平均错误概率PE任意小。