设有M种信源码字要在信道中传送,信道的输入符号序列(即码字)为C=(xn-1,xn-2,…,x0),其中码元xi(i=n-1,n-2,…,0)为r元码。如何在rn个码字中选用M个许用码字来代表信源输出的消息,才能以任意小的错误概率传送,这就需要编码。这种编码实质上是针对信道特性对信源输出进行编码,以使信源与信道相匹配,所以称为信道编码。

定理8.1(有噪信道编码定理)　若一个离散无记忆信道[X,P(y x),Y]的信道容量为C,当信息传输率R＜C时,只要码长n足够大,总可以找到一种编码和相应的译码规则,使平均错误概率PE任意小。

定理8.1又称为香农第二定理,其含义是:设信道有r个输入符号和s个输出符号,其信道容量为C。对信道进行n次扩展,输入到扩展信道的码字(即经过信道编码得到的码字)长度为n,因此有rn个可供选择的码字。从rn个符号集中找到M个码字(即M个许用码字,用来代表M个等概出现的消息,且M≤2n(C-ε),ε为任意小的正数)组成一码表。需要指明的是,定理中的等概消息数应理解为信源扩展后经信道编码输出的码字数;定理中的信道容量C应该以“比特/码元”为单位(即对数底为2),它与2n(C-ε)中的底数2相对应。这样编码后,信息传输率

则存在相应的译码规则,使有噪信道中传输信息的平均错误概率任意小。

定理8.1说明信道容量C是保证无差错传输信息传输率R的理论极限值。对于一个固定的信道,信道容量C是一定的,它是衡量信道质量的一个重要物理量。

关于有噪信道编码定理有以下几点说明。

①有噪信道编码定理指出高效率和高可靠性的编码是存在的,并给出了信道编码的理想极限性能,为编码理论和技术的研究指明了方向。

②定理证明过程中采用随机编码,在信道输入端的Xn集中随机地选取经常出现的2nR个高概率序列作为码字,数量很大,难以寻找到好码。

③定理证明过程中采用最大似然译码准则。在接收端,序列Yn集将映射到M个消息集中。(www.daowen.com)

④可以证明:当R＜C时,平均错误概率PE满足不等式

其中,n为码长;E(R)称为可靠性函数或随机编码指数,它在0＜R＜C范围内是一个非增的非负函数,可靠性函数E(R)与R的关系如图8.3所示。可见,为了实现可靠通信,可以采用增大可靠性函数E(R)或增加码长n的方法;而且随着码长n的增加,PE按指数规律下降到任意小的值。

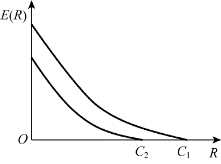
图8.3　可靠性函数E(R)与R的关系示意图

定理8.2(有噪信道编码逆定理)　若一个离散无记忆信道[X,P(y x),Y]的信道容量为C,当信息传输率R＞C时,无论码长n多么大,总也找不到一种编码和相应的译码规则,使平均错误概率PE为任意小。

需要指明的是,有噪信道编码定理及其逆定理对连续信道和有记忆信道同样成立。

综上所述,在任何信道中,信道容量是一个明显的分界点,它是保证信息可靠传输的最大信息传输率。香农第二定理从理论上指出:任何信道,只要信息传输率R接近于C,就有可能近似无差错传输,此差错可通过适当的编码来实现。也就是说,存在一种编码方式,通过不可靠的信道可实现可靠的传输,且有可能使信息传输速率接近于香农容量。这对实际信息传输工程有着重要的理论指导意义,多年来,编码理论家一直在探索逼近香农极限的实用码,即以接近香农信道容量的信息速率进行通信,而且近似无差错。近二十年来,信道编码取得可喜进展,信道编码采用Turbo码或LDPC码的通信系统,信息速率接近于香农容量时,在近似无差错(误比特率为10-5)条件下,它所要求的Eb/N0值仅与理想值相差不到1dB,且其编译码可实现。