设一个二元对称信道的转移概率矩阵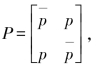错误转移概率为p=0.01。如果在发送端直接将信息序列送入信道(即不进行信道编码,可以看作是一种特殊的信道编码),译码规则为:接收符号为“1”,则译成发送符号为“1”;接收符号为“0”,则译成发送符号为“0”。则错误概率为

如果译码规则为:接收符号为“1”,则译成发送符号为“0”;接收符号为“0”,则译成发送符号为“1”。则平均错误概率

可见,错误概率不仅与信道的传输特性有关,也与译码规则有关。

现在来定义译码规则。设离散单符号信道的输入符号集为X={a1,a2,…,ar},输出符号集为Y={b1,b2,…,bs},如果对每一个输出符号bj都有一个确定的单值函数F(bj),使bj对应于一个输入符号ai,则称这样的函数为译码规则。译码规则就是设计一个函数F(bj),表示为

显然,对于r个输入s个输出的信道而言,按上述定义得到的译码规则不是唯一的。在这些译码规则中,不是每一种译码规则都是合理的。译码规则的选择应该根据什么准则呢?一个很自然的准则是使错误概率最小。因此在讨论译码规则的选择之前,首先来介绍如何计算错误概率。

在确定译码规则F(bj)=ai后,若信道输出端接收到的符号为bj,则一定译成ai。如果发送的就是ai,这就是正确译码;反之为错误译码。那么,收到符号bj的条件下正确译码的条件概率为

则错误译码的条件概率为

其中,e表示除了ai之外的所有输入符号的集合。

错误概率PE应是错误译码的条件概率对Y空间取统计平均。即

定义8.1　选择译码函数

使之满足条件

则称为“最大后验概率(MAP)准则”或“最小错误概率准则”。

这时,式(8.6)等价为

定义8.2　选择译码函数

使之满足条件

或记为

最大似然译码准则是实际应用中最常用的一种译码规则。它不再依赖先验概率P(ai),但是只有当先验概率相等时,最大似然译码准则和最大后验概率准则才是等价的。如果先验概率未知或不等概,仍采用这个准则,不一定能使平均错误概率PE最小。(www.daowen.com)

根据译码准则,可写出平均错误概率。

可见,无论采用最大后验译码准则还是最大似然译码准则,PE是在联合概率矩阵[P(aibj)]中先求每列除去F(bj)=a*所对应的P(a*bj)以外所有元素的和,然后再对各列求和。

如果先验等概,式(8.10)可写成

式(8.11)的求和是除去信道转移矩阵每列F(bj)=a*对应的那个元素之后,再对矩阵中其他元素求和。

【例8.1】设有一个离散信道,信道转移矩阵

(1)试按照“最大后验译码准则”确定译码规则,并计算相应的译码错误概率。

(2)试按照“最大似然译码准则”确定译码规则,并计算相应的译码错误概率。

解:(1)因为最大后验译码准则等价为

可知需要先计算联合概率P(aibj)。因为

所以,由最大后验译码准则得到的译码规则为

这时的译码错误概率为

(2)已知信道矩阵,由最大似然译码准则得到的译码规则为

这时的译码错误概率为

可见,先验概率不相等时,最大似然译码准则和最大后验译码准则不等价。

平均错误概率PE与译码规则有关,而译码规则又与信道特性有关。由于信道中存在噪声,导致输出端发生错误,并使接收到输出符号后,对发送的符号还存在不确定性。可见,平均错误概率PE与信道疑义度H(X Y)有关。两者之间的关系表示为

其中,r是输入符号集的个数,H(PE)是错误概率PE的熵。该不等式由费诺第一个证明得出,所以称为费诺不等式。费诺不等式给出了平均错误概率的下限,它表明:当作了译码判决后所保留的关于信源X的平均不确定性可分为两部分。一部分是接收到Y后是否产生错误概率PE的不确定性H(PE);另一部分是当判决错误(错误概率为PE)发生后,到底是(r-1)个输入符号中的哪一个造成错误的不确定性,它是(r-1)个输入符号不确定性的最大值log(r-1)与错误概率PE的乘积,即PElog(r-1)。