针对二元对称信道,以简单重复编码为例,说明通过信道编码可以降低平均错误概率的原理。

将信源符号重复发送n次,并在接收端采用相应的译码方法,就有可能减少错误概率,从而通过牺牲有效性来换取可靠性的提高。比如信源发出两种符号A和B,分别用“0”和“1”表示。在发送端,信源符号为“0”(或“1”)时,则重复发送三个“0”(或“1”)。即用“000”代表消息A,“111”表示B。由于3位的二元码有23=8种组合,除去2组许用码字(“000”和“111”)外,余下的6组001、010、100、011、101、110不允许使用,称为禁用码字。此时,如果传输中产生一位错误,接收端将收到禁用码字,可以检测出传输有错,而且还可以根据“大数法则”来译码,即3位码字中如有2个或3个“0”,则译为消息A;如有2个或3个“1”,则译为消息B。所以,此时可以纠正一位错码。如果在传输中产生两位错码,接收端也将收到禁用码字,译码器仍可检错,但是不再具有纠错能力。如果在传输中产生三位错码,接收端收到是许用码字,这时不再具有检错能力。因此,这时的信道编码具有检出两位和两位以下错码的能力或者具有纠正一位错码的能力。

这时信道可以看作是二元对称信道的三次扩展信道,信道输入是码长为3的许用码字αi(i=1,2),输出是码长为3的接收码字βj(j=1,2,…,8),如图8.2所示。

对应的信道矩阵为

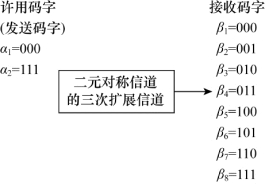
图8.2　(3,1)重复码的信道模型

一般来说,信道的错误转移概率根据最大似然准则进行译码(参考下节),译码函数为

所以,当输入等概,p=0.01时,纠1位错码的n=3的重复码的译码错误概率为(www.daowen.com)

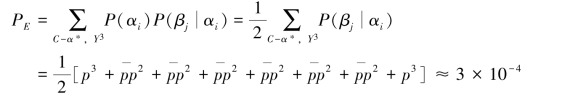
可见,采用简单重复编码,即使只能纠正这种码字中1个错误码元,当p=0.01时,可以使平均错误概率从0.01下降到3×10-4。这表明信道编码具有较大的实用价值。

如果进一步增大重复次数n,则会继续降低平均错误概率PE。可以算出

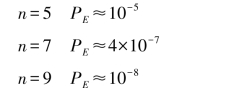
当n很大时,平均错误概率很小,但同时带来一个新问题,信息传输率大大减小。编码后的信息传输率(也称码率)表示为其中,M表示许用码字的个数(即输入信道编码器的消息个数),logM表示消息集在等概条件下每个消息携带的平均信息量(底数为2时,单位为比特)。n是编码后码字的长度。

当M=2时,采用n位重复码,得到的码率为

可见信息传输有效性和可靠性是矛盾的。