对于某一信源和某一码元集来说,若有一个唯一可译码,其平均长度L不大于其他唯一可译码的平均长度,则称此码为最佳码(紧致码)。具有以下性质:

(1)若pi＞pj,则Li≤Lj。即概率大的信源符号所对应的码长不大于概率小的信源符号所对应的码长。

(2)对于二元最佳码,两个最小概率的信源符号所对应的码字具有相同的码长。而且这两个码字,除了最后一位码元不同之外,前面各位码元都相同。

1952年霍夫曼提出了一种构造最佳码的方法。所得的码字是即时码,在所有的唯一可译码中,它的平均码长最短,是一种最佳变长码。

二元霍夫曼码的编码步骤如下:

(1)将q个信源符号si按出现概率P(si)递减次序排列起来;

(2)取两个概率最小的符号,其中一个符号编为0,另一个符号编为1;并将这两个概率相加作为一个新符号的概率,从而得到包含(q-1)个符号的新信源,称为缩减信源。

(3)把缩减信源中的(q-1)个符号重新以概率递减的次序排列,重复步骤(2)。

(4)依次继续下去,直至所有概率相加得到1为止;

(5)从最后一级开始,向前返回,得到各个信源符号所对应的码元序列,即相应的码字。

【例7.5】某离散无记忆信源共有8个符号消息,其概率空间为

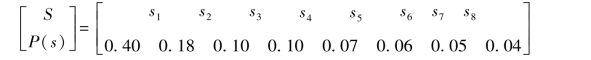
(1)计算信源熵H(S)和信源的冗余度。

(2)进行霍夫曼编码,并计算编码后的信息传输率、编码效率和码冗余度。

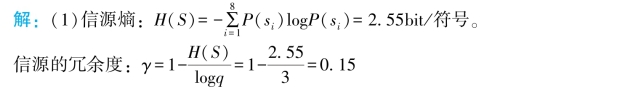
(2)

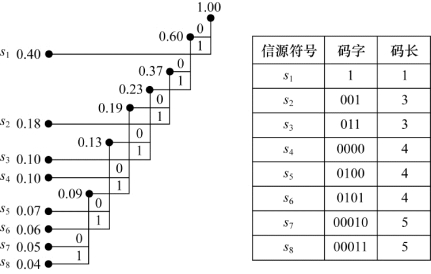
说明:

1.霍夫曼编码方法得到的码并非唯一

(1)每次对信源缩减时,赋予信源最后的两个概率最小的符号,用0和1是可以任意的,所以可以得到不同的霍夫曼码,但是不会影响码字的长度。

(2)对信源进行缩减时,两个概率最小的符号合并后的概率与其他信源符号的概率相同时,这两者在缩减信源中进行概率排序,其位置放置次序是可以任意的,故会得到不同的霍夫曼码。这时将影响各码字的长度,但是平均码长相同。一般将合并后的概率放在上面,这样可以获得较小的码方差。

2.需要大量的存储设备来缓冲码字长度的差异,这是码方差小的码质量好的原因。

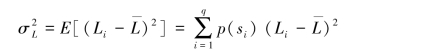
【例7.6】某离散无记忆信源共有5个符号消息,其概率空间为

两种霍夫曼编码如图7.5所示。

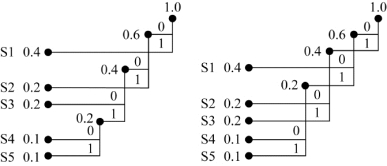
图7.5　两种霍夫曼编码

两种码有相同的平均码长和编码效率,但第一种霍夫曼编码的码长方差比第二种霍夫曼编码的码长方差小许多,所以第一种霍夫曼编码的质量较好。

进行霍夫曼编码时,应把合并后的概率总是放在其他相同概率的信源符号之上,以得到码长方差最小的码。

【例7.7】设离散无记忆信源的概率空间为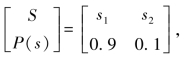对信源进行N次扩展,采用二元霍夫曼编码。当N=1,2,3,4,∞时的平均码长和编码效率为多少?

解:(1)N=1时,将s1编成0,将s2编成,1,则

又因为信源熵H(S)=H(0.9,0.1)=0.469比特/符号(www.daowen.com)

所以编码效率

(2)如果对长度N=2的信源序列进行霍夫曼编码,编码结果如下表所示。

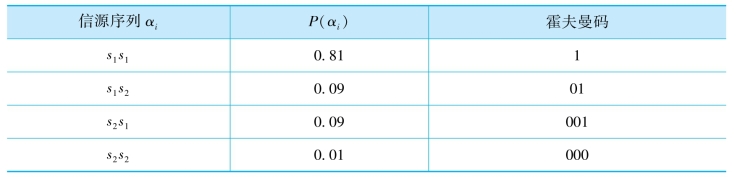
此时,信源序列的平均码长

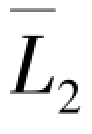=1×0.81+2×0.09+3×(0.01+0.09)=1.29二元码符号/信源符号序列

则单个符号的平均码长

所以对长度为2的信源序列进行变长编码,编码后的编码效率

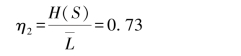
(3)用同样的方法进一步将信源序列的长度增加,对N=3,N=4的序列进行最佳编码,可得编码效率为

显然,随着信源序列的长度增加,编码效率越来越接近1。

(4)N=∞时,由香农第一定理,必然存在唯一可译码,使

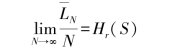
而霍夫曼编码为最佳码,即平均码长最短的码,故

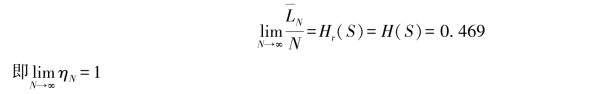
r元霍夫曼码

二元霍夫曼编码方法可以推广到r元编码中来。不同的是每次将r个概率最小的符号合并成一个新的信源符号,并分别用0,1,…,(r-1)等码元表示。

为了使短码得到充分利用,平均码长最短,必须使最后一步的缩减信源有r个信源符号,因此对于r元编码,信源的符号个数q必须满足

其中θ表示缩减的次数,(r-1)为每次缩减所减少的信源符号个数。

对于r元码,q为任意整数时不一定能找到一个θ满足式(7.2)。若q不满足时,不妨人为地增加一些概率为零的符号。设增加t个信号源符号Sq+1,Sq+2,…,Sq+t

并使它们对应的概率为零,即P(Sq+1)=P(Sq+2)=…=P(Sq+t)=0

设n=q+t,此时n满足n=(r-1)θ+r

然后取概率最小的r个符号合并成一个新符号,并把这些符号的概率相加作为该节点的概率,重新按概率由大到小顺序排队,再取概率最小的r个符号并列;如此下去直至树根。

【例7.8】已知离散无记忆信源

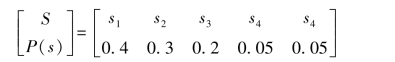
试编出三元霍夫曼码和四元霍夫曼码,并计算编码效率。

解:三元霍夫曼码和四元霍夫曼码如下所示。

说明:要发挥霍夫曼编码的优势,一般情况下,信源符号数应远大于码元数。本例中,若编五元码,只能对每个信源符号赋予一个码元,相当于没有编码,当然无压缩可言。

霍夫曼码为最佳码,其平均码长满足