在变长编码中,码长Li是变化的,根据信源符号的统计特性,对概率大的符号用短码,而对概率小的符号用较长的码,这样平均码长L 就可以降低,从而提高编码效率。当平均码长L =H(S)时,编码效率达到1。是否此时的平均码长就是无失真信源编码的最小值?无失真变长信源编码定理将回答这个问题。

定理7.2(单个符号的无失真变长编码定理)　一个符号熵为H(S)的离散无记忆信源,每个信源符号用r进制码元进行变长编码,一定存在一种无失真编码方法,构成唯一可译码,其码字平均长度L满足

定理7.3又称为香农第一定理,前面的定理7.2可以看作是它的特例。香农第一定理的结论同样适用于平稳遍历的有记忆信源。

香农第一定理是香农信息论的主要定理之一。定理指出:要实现无失真的信源编码,每个信源符号的平均码长的极限值就是原始信源的熵值Hr(S)。当编码的平均码长小于信源的熵值,则唯一可译码不存在,在译码时必然带来失真或差错。同时它还表明:通过对扩展信源进行变长编码,当N→∞时,平均码长可达到这个极限值。

香农第一定理也可陈述为:若R′＞H(S),就存在唯一可译码变长编码;若R′＜H(S),唯一可译变长编码不存在,不能实现无失真的信源编码。

编码效率: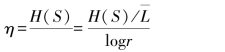

二元编码时,编码效率:(www.daowen.com)

由香农第一定理可以看出:当平均码长达到极限值时,编码效率为1。这时编码后的信道信息传输率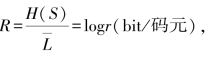即r个码符号独立等概分布,达到最大熵。

无失真信源编码的实质就是对离散信源进行适当的变换,使变换后新的码元概率尽可能等概,以使每个码元平均所含的信息量达到最大。

请思考以下问题:

(1)为什么一般不采用定长码,而采用变长码?

(2)无失真定长信源编码定理(或无失真变长信源编码定理)指出:平均码长的极限值为多少?

(3)无失真变长信源编码定理指出:当编码效率达到1时,这时编码后的信道信息传输率R为多少?此时变换后新的码元概率分布如何?