【例7.1】设一个离散无记忆信源的概率空间为

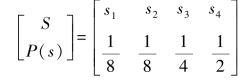
采用两种信源编码方案编出的码字如下表所示。

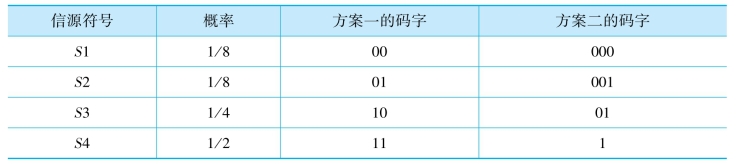
试问方案一和方案二的码字哪个有效性较好?

1.定长码和变长码

如果码字集合C中所有码字的码长都相同,称为定长码(或等长码)。反之,如果码字长度不同,则称为变长码。

2.二元码

如果码元集X={0,1},对应的码字称为二元码。

3.奇异码和非奇异码(www.daowen.com)

一般来说,无论是定长码还是变长码,如果码字集合C中含有相同码字,则称为奇异码。否则称为非奇异码。非奇异性是正确译码的必要条件。

4.唯一可译码和非唯一可译码

如果一种码的任何一串有限长的码元序列,只能被唯一地译成对应的信源符号序列,则称该码为唯一可译码。否则称为非唯一可译码。为了实现无失真信源编码,必须采用唯一可译码。

例如,{0,10,11}是一种唯一可译码,因为任意一串有限长的码序列,比如10001100,只能被分割为{10,0,0,11,0,0,},任何其他分割方法都会产生一些非定义的码字。

5.即时码和非即时码

在唯一可译码中有一类码,它在译码时无须参考后续的码元就能立即做出判断,译成对应的信源符号序列,则这类码称为即时码。否则称为非即时码。即时码不能在一个码字后面添上一些码元构成另一个码字,即任一码字都不是其他码字的前缀,所以它也称为异前缀码。即时码一定是唯一可译码,但唯一可译码不一定是即时码。

非奇异码,唯一可译码和即时码三者之间的关系如图7.3所示。

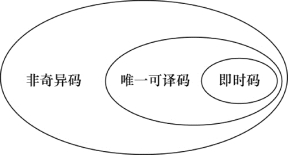
图7.3　非奇异码、唯一可译码和即时码三者之间的关系