香农公式给出了加性高斯白噪声通信系统的信道容量,它是无差错传输下可以达到的极限信息传输速率。鉴于香农公式在信息论中的重要作用,下面对香农公式作深入讨论。

1.当带宽W一定时,信噪比SNR与信道容量Ct成对数关系。若SNR增大,Ct就增大,但增大到一定程度后会趋于缓慢。这说明增加输入信号功率有助于容量的增大,但该方法是有限的;另方一面降低噪声功率也是有用的,当N0→0时,Ct→∞,即无噪声信道的容量为无穷大。

2.当输入信号功率PS一定,增加信道带宽,容量可以增加,但到一定阶段后增加变得缓慢,因为当噪声为加性高斯白噪声时,随着W的增加,噪声功率N0W也随之增加。

当对数底数取2,即Ct单位为比特/秒时,信道容量为

3.Ct一定时,带宽W增大,可以降低对信噪比SNR的要求,即两者是可以互换的。若有较大的传输带宽,则在保持信号功率不变的情况下,可允许较大的噪声,即系统的抗噪声能力提高。

需要说明的是,带宽和信噪比的互换过程不是自然而然实现的,必须通过具体的编码和调制等通信技术来实现。理想通信系统如图6.4所示,其中发送设备对信源输出的原始信号进行理想调制或编码,接收设备对信道输出的信号进行理想解调或解码。设原始信号的带宽为Bo,进入信道的信号带宽为Bi,接收设备的输入信噪比为SNRi,接收设备的输出信噪比为SNRo。因为接收设备完成发送设备的反变换,所以接收设备的输入信号带宽为Bi,输出至信宿的带宽为Bo。

图6.4　理想通信系统的示意图

这样,接收设备的输入信息速率为

假设接收设备不引入信息损失,则接收设备的输入信息速率和输出信息速率相同,即

而

即

因此当SNRi＞＞1,SNRo＞＞1时,有(www.daowen.com)

可见,在理想通信系统中,增加宽带可以明显地改善输出信噪比,信噪比的改善与带宽比成指数关系。实际通信系统如扩频系统、宽带调频系统和脉冲编码调制,就是利用了这个原理。比如扩频通信将所需传送的信号扩频,使之远远大于原始信号带宽,以增强抗干扰的能力。需要指明的是,香农公式只证明了理想通信系统的“存在性”,却没有指出这种通信系统的实现方法。到目前为止,还没有一种实际通信系统能达到式(6.26)表明的理想结果。但香农公式的伟大之处在于从理论上给出了带宽和信噪比进行互换的可能性,而后人正是沿着这个方向,不断努力去发现并实现这种互换的具体方法。

4.连续信道编码定理

和离散信道一样,连续信道的容量同样是信道中可靠通信的最大信息速率。香农第二编码定理同样适合于连续信道。

利用关系式PS=RtEb,其中Eb代表每比特的能量。可得

其中,Rt/W为频带利用率,Eb/N0为比特信噪比。

因此,为了保证可靠通信,实际通信系统的Rt/W和Eb/N0应满足

该关系式对任何通信系统都成立,当Rt/W→0时,得到可靠通信所要求的Eb/N0的最小值,即-1.6dB香农限,频带利用率Rt/W随着比特信噪比Eb/N0的变化的曲线如图6.5所示。理论上,在该曲线以下的任何点通信是可能的,而在其上的任何点通信是不可能的。

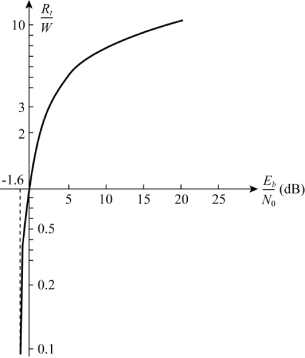
图6.5　频带利用率与比特信噪比的关系曲线

注意:在任何信道中,信道容量是一个明显的分界点,它是保证信息可靠传输的最大信息传输率。香农第二定理从理论上指出任何信道,信息传输速率Rt接近于Ct的最优抗干扰编码是存在的、可能的。这对实际信息传输工程有着重要的理论指导意义。

【例6.4】给定比特信噪比Eb/N0=22dB,信道带宽为1MHz时,能否可靠传输信息速率为10Mbit/s的数据?

解:根据式(6.29),信道带宽为1MHz时Eb/N0的最小值为

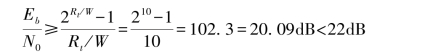
所以通过适当的编码方式可以实现无差错传输。