讨论完连续信源问题后,现在讨论连续信道的平均交互信息。

对于限时T,限频F的连续信源{x(t)},可以转化为时间间隔Δ=1/2F的N(=2FT)维随机矢量X=X1X2…XN。每一时刻的随机变量Xi(i=1,2,…,N)取值区间均为[a,b]。传递概率密度函数为p(y/x),信道输出端输出相应的随机变量Yi(i=1,2,…,N),其取值区间均为[a′,b′],组成随机矢量Y=Y1Y2…YN。从整体上看待信息传递过程,相当于形成了一个新的信道,输入输出均为N维随机矢量,如图6.1所示。

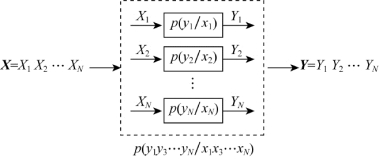
图6.1　多维无记忆信道模型

若N次扩展信道(X-Y)的传递概率密度函数p(y/x)=p(y1y2…yN/x1x2…xN)可由单维连续信道(X-Y)的传递概率密度函数p(y/x)表示,并等于各时刻单维连续信道(X-Y)的传递概率密度函数p(yi/xi)(i=1,2,…,N)的连乘

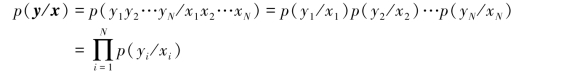
则信道(X-Y)称为无记忆连续信道。

对于无记忆连续信道的N次扩展信道,有

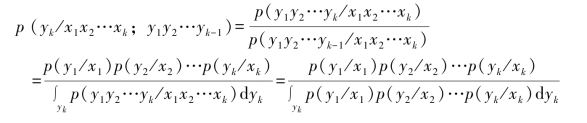
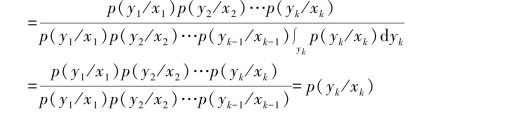
说明,时刻k的输出Yk只依赖于同一时刻k的输入Xk,与k时刻之前的输入序列和输出序列无关,这就是无记忆连续信道的“无记忆”性,又有

这说明,时刻k之前的k-1个输出只与k之前的k-1个输入有关,而与下一时刻的输入Xk无关。这就是无记忆连续信道的“无预感”性。

下面给出反映N次扩展信道(X-Y)的平均交互信息量I(X;Y)与单维连续信道(XY)在各时刻传递的平均交互信息量I(Xi;Yi)之间关系定理。

定理6.3连续无记忆信道(X-Y)的N次扩展信道(X-Y)的平均交互信息量。

【证明】连续无记忆信道(X-Y)的N次扩展信道(X-Y)的平均交互信息量

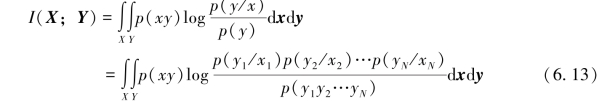(www.daowen.com)

输入随机矢量X=X1X2…XN中每一时刻随机变量Xi(i=1,2,…,N)通过无记忆信道(X-Y),输出随机变量Yi(i=1,2,…,N)的平均交互信息量I(Xi;Yi)(i=1,2,…,N)之和

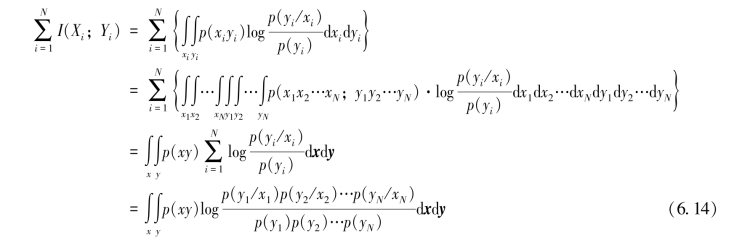
由式(6.13)和式(6.14),有

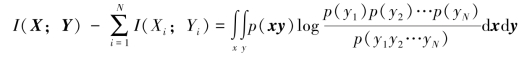
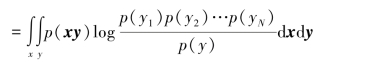
考虑到“底”大于1的对数函数的上凸特性,有

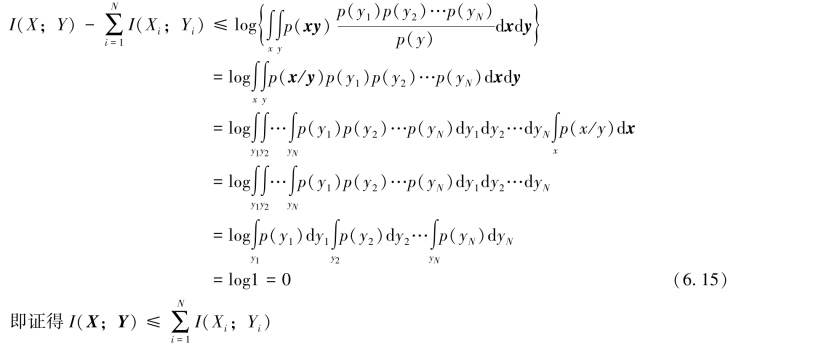
另一方面,对于无记忆信道,当信源无记忆时,即

有

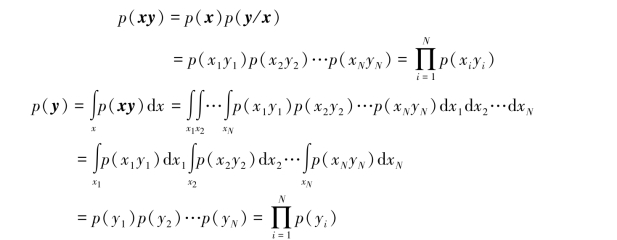
即有p(y1y2…yN)=p(y1)p(y2)…p(yN)

即

如果信源在N个时刻的概率密度函数相同,即p(x1)=p(x2)=…=p(xN)=p(x),则各时刻k(k=1,2,…,N)的连续随机变量Xk(k=1,2,…,N)通过连续信道(X-Y)的平均交互信息量I(Xk;Yk)(k=1,2,…,N)都等于连续信源X通过连续信道(X-Y)的平均交互信息量I(X;Y)。这样,由式(6.16),有I(X;Y)≤NI(X;Y),进一步,若信源无记忆,则有