设连续信道的输入X:[a,b],输出Y:[a′,b′],信道转移概率p(y/x),如图5.9所示。

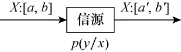
图5.9　连续信道模型

根据单维连续信道平均互信息的定义,有

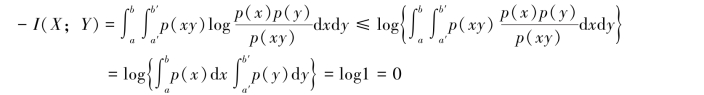
说明I(X;Y)≥0,只有当p(xy)=p(x)p(y),即输入、输出变量之间统计独立时,I(X;Y)=0。

定理5.4　传递概率密度函数为p(y/x)的连续信道的平均交互信息量I(X;Y),是输入连续信源X的概率密度函数p(x)的∩型凸函数。

图5.10　同一信道下的三种不同输入信源

【证明】如图5.10所示,设信道有三种信源输入概率密度分别为p1(x),p2(x),p3(x)=αp1(x)+βp2(x)　(0＜α,β＜1,α+β=1)

对p1(x)分布的平均互信息

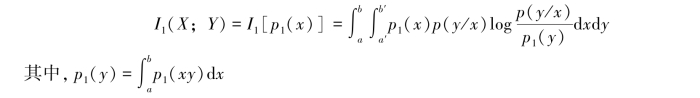
对应p2(x)分布的平均互信息(www.daowen.com)

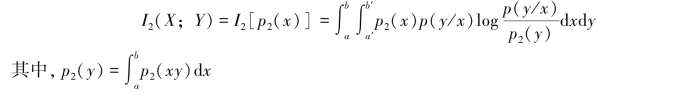
对p3(xy)分布的平均互信息

根据∩型凸函数的数学特性,上式右边第一项可改写为

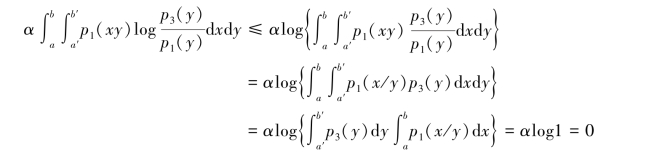
右边第二项可以改写为

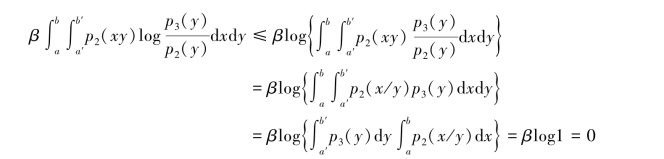
证得αI1[p1(x)]+βI2[p2(x)]≤I3[αp1(x)+βp2(x)]

根据∩型凸函数的定义,证得I[p(x)]是p(x)的∩型凸函数。

对于给定信道,通过变动连续信源的概率密度函数p(x),总可以找到一种信源,使连续信道的平均互信息量达到极大值。这个极大值就是连续信道的信道容量。