离散信源通过具有一一对应的确定函数关系变换后,变换前后熵不发生改变,但连续信源相对熵经过变换后不具备此性质。对于如图5.6所示的连续信源坐标变换,有如下定理。

图5.6　连续信源坐标变换

定理5.3　取值区间为[a,b],概率密度函数为p(x),相对熵为h(X)的连续信号源X,经确定的单值函数y=y(x)[x=x(y)]变换后,连续输出随机变量Y的相对熵h(Y)=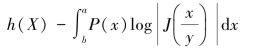

如下所示,设X→Y为一一对应变换

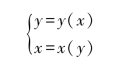
变换前信源X的信源空间为

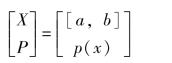
变换后随机变量Y的取值区间为[a′,b′],概率密度函数为q(y),则有得到变换后输出随机变量Y的熵

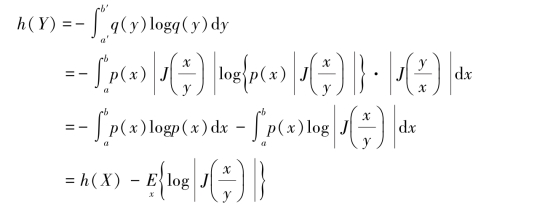
经过坐标变换系统,引起相对熵的变化,其变化量等于雅可比行列式绝对值的对数,在原坐标系统中的统计平均值,这也是h(X)取名为相对熵的重要原因之一。

【例5.2】图5.7中信息变换装置的变换函数关系是Y=σX+a连续信源X在整个实轴R:(-∞,∞)取值,其概率密度函数为

试求信息变换装置输出连续随机变量Y的概率密度函数q(y)和相对熵h(Y)(www.daowen.com)

图5.7　信息变换装置

解:由

得

则雅可比行列式绝对值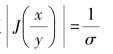

输出随机变量Y的概率密度函数

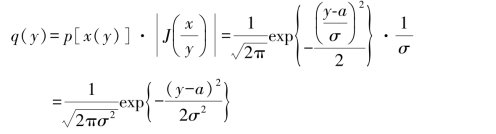
连续信源X的连续熵

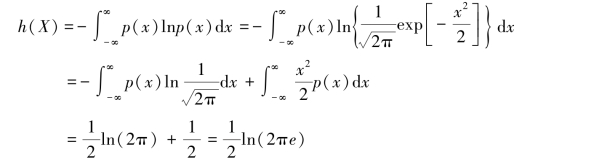
输出连续随机变量Y的连续熵

表明输出Y相对熵只与系统增益σ有关。