设单维连续信道的输入区间[a,b],输出区间[a′,b′]。信道转移概率密度函数p[y/x](x∈[a,b],y∈[a′,b′]),而且对所有的x∈[a,b],都有
![]()
一个给定的单维连续信道可由图5.2表示,称为正向信道,图5.3称为反向信道,正向信道和反向信道是同一通信系统的两种不同的表达形式。
![]()
图5.2 正向信道
![]()
图5.3 反向信道
现在求解连续随机变量X和Y通过连续信道传递的平均交互信息量I(X;Y)。
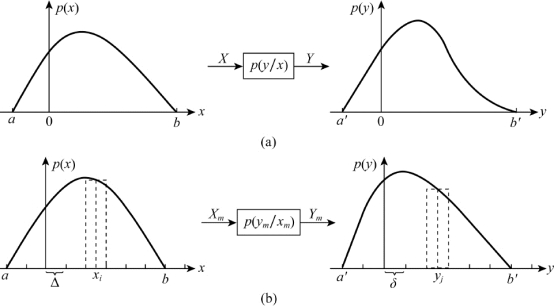
图5.4 连续信道的离散化

根据积分中值定理,在区间[a+(i-1)Δ,a+iΔ]中,必存在一个xi,且有
![]()
根据上节讨论,连续信源X的信息熵

根据积分中值定理,在区间[a′+(j-1)δ,a′+jδ]j(j=1,2,…,m)内,总可找到一个值yj(j=1,2,…,m),有
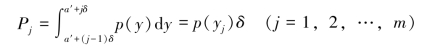
在整个区间[a′,b′]内连续取值的连续随机变量Y,即可量化为取m个离散值yj(j=1,2,…,m)的离散随机变量Ym。
3.在对X量化为Xn,Y量化为Ym的基础上,对联合概率密度函数p(xy)和反向传递概率密度函数p(x/y)进行量化。
单维连续信源X落在第i(i=1,2,…,n)区间[a+(i-1)Δ,a+iΔ]、输出连续随机变量Y落在第j(j=1,2,…,m)区间[a′+(j-1)δ,a′+jδ]的联合概率
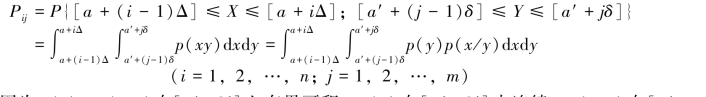
因为p(y),p(x/y)在[a′,b′]上有界可积,p(y)在[a′,b′]内连续,p(x/y)在[a′,b′]内连续且不变号,根据有关数学定理,可有(www.daowen.com)
![]()
再根据二重积分中值定理,可有
![]()
其中,(xij,yij)是x-y平面中[a+(i-1)Δ,a+iΔ]×[a′+(j-1)δ,a′+jδ]二维区域中的一点,当分层间隔Δ→0,δ→0(即n→∞,m→∞)时,yij和yj可趋于同一点,并以yj表示;xij和xi可趋于同一点,并以xi表示。如图5.5所示。
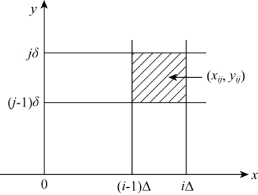
图5.5 联合概率密度函数的离散化
在输出连续随机变量Y落在第j(j=1,2,…,m)区间[a′+(j-1)δ,a′+jδ]的前提下,推测单维连续信源X落在第i(i=1,2,…,n)区间[a+(i-1)Δ,a+iΔ]的后验概率
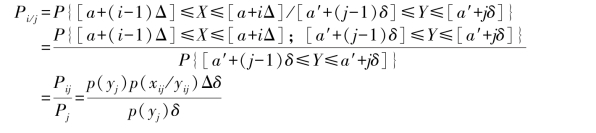
![]()
4.(Xn-Ym)是离散信道,信道疑义度H(Xn/Ym)为
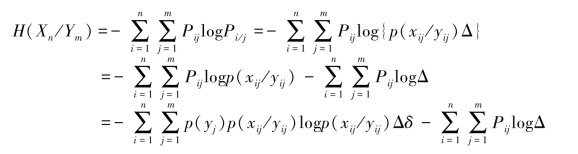
进一步改写为
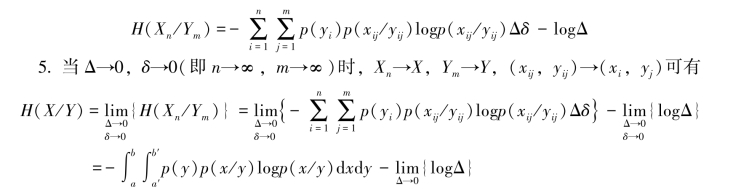
令上式中
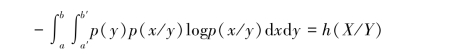
并把h(X/Y)称为单维连续信道的相对疑义度,则有
![]()
最后得到单维连续信道(X→Y)的平均交互信息量
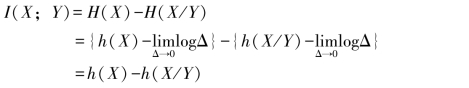
连续信道平均交互信息量也有类似离散信道的三种不同表达形式
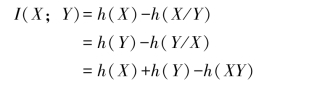
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






