N次扩展信道(X-Y)的平均交互信息量I(X;Y),必然与信源X=X1X2…XN各时刻的随机变量Xk(k=1,2,…,N)单独通过信道(X-Y)的平均交互信息量I(Xk;Yk)(k=1,2,…,N)的和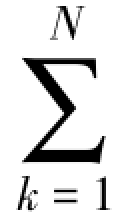I(Xk;Yk)有关。

根据平均交互信息量的一般定义,可得图4.7所示N次扩展信道(X-Y)的平均交互信息量的三种表达式

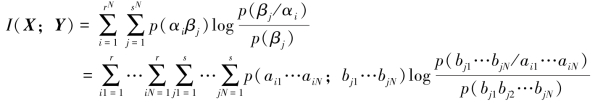
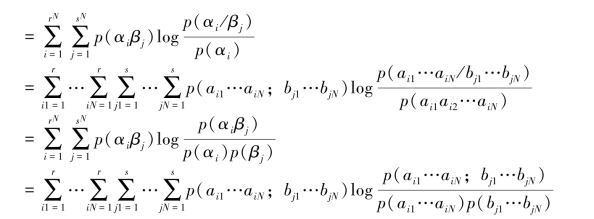
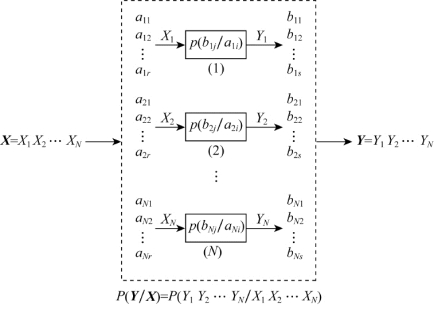
图4.7　扩展信道模型

定理4.4　一般离散信道[X,P(y/x),Y]中,设X=(X1X2…XN),Y=(Y1Y2…YN),其中

且有x∈X,y∈Y;xi∈Xi,yi∈Yi　i=1,2,3,…,N

(1)当信道是无记忆的,即信道传递概率满足

则有

(2)当信道的输入信源是无记忆的,即满足

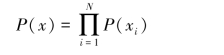
则有

(3)当信道和信源都是无记忆时,上述两条件都满足

则有

【证明】(1)设信道输入和输出随机序列X和Y的一个取值为αk=(ak1ak2…akN),aki∈{a1,…,ar}(i=1,2,…,N),和βh=(bh1bh2…bhN),bhi∈{b1,…,bs}(i=1,2,…,N)。根据平均互信息的定义得X和Y的平均互信息

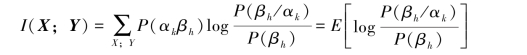
式中,E[·]表示在XY的联合空间中求统计平均。因信道是无记忆的,得

另一方面

上式E[·]也是对XY的联合空间求均值。所以

(www.daowen.com)

根据詹森不等式,得

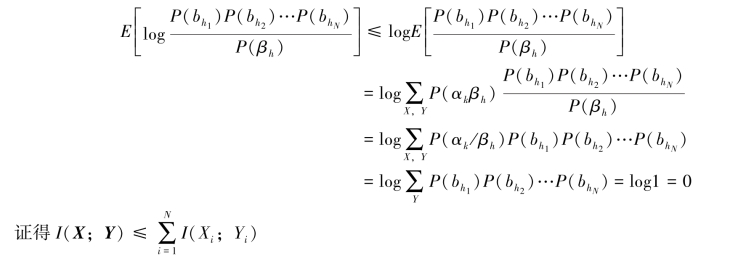
当信源是无记忆时,则有P(αk)=P(ak1)P(ak2)…P(akN),而

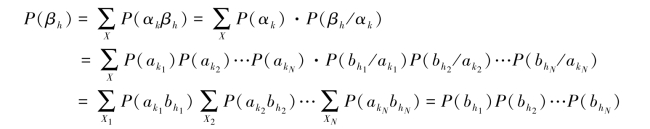
因此式(4.8)等号成立。

(2)根据平均互信息定义得X和Y的平均互信息

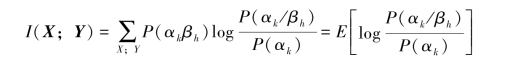
式中,αk和βh是随机矢量X和Y的一个取值,αk=(ak1ak2…akN),aki∈{a1,…,ar}(i=1,2,…,N),和βh=(bh1bh2…bhN),bhi∈{b1,…,bs}(i=1,2,…,N)。因信源是无记忆的,即随机序列X中每一分量是相互独立的,因而

因此得

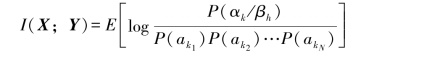
式中,E[·]表示对XY的联合空间求均值。

另一方面

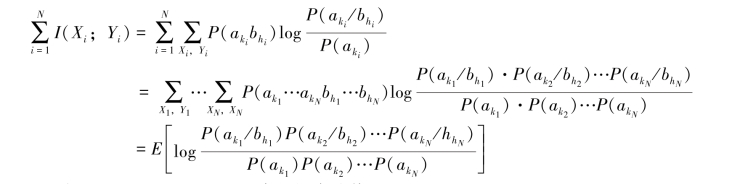
上式E[·]也是对XY的联合空间求均值。所以

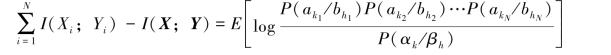
根据詹森不等式,得

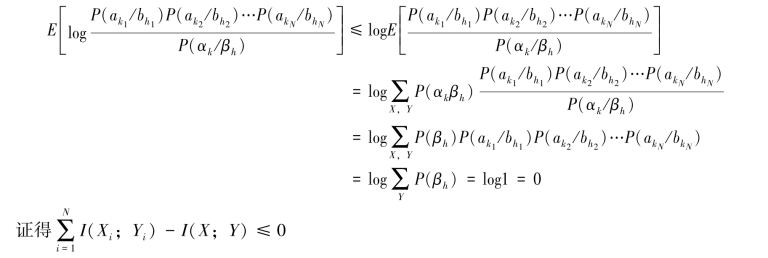
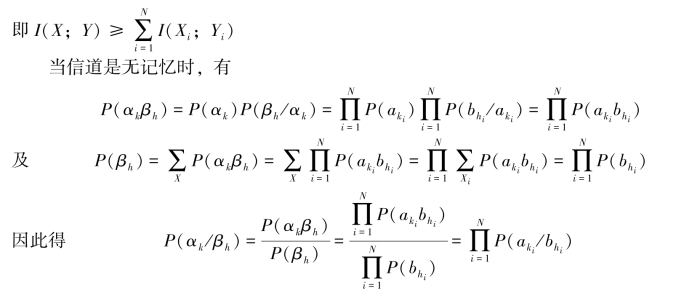
所以式(4.9)的等号成立。

(3)从上述(1)和(2)的证明中可知,若信源与信道都是无记忆的,则式(4.8)和式(4.9)同时满足,即它们的等式成立

上述证明也可以运用平均联合互信息和平均条件互信息的表达式来证明。

特别地,当Xi(1,2,…,N)取自于同一符号集且概率分布相同,Yi(1,2,…,N)也取自同一符号集。则有

当信源和信道都无记忆时,有