若N次扩展信道的传递概率P(Y/X)=P(Y1Y2…YN/X1X2…XN),等于N个时刻单符号离散信道(X-Y)的传递概率p(Yk/Xk)(k=1,2,…,N)的连乘,即

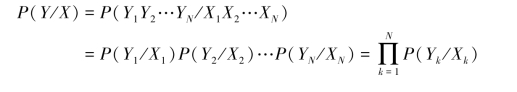
即

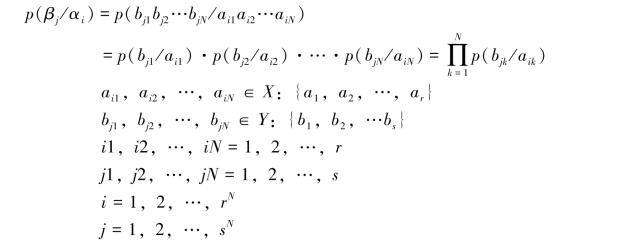
则单符号离散信道(X-Y)称为离散无记忆信道,相应的N次扩展信道(X-Y)称为离散无记忆信道(X-Y)的N次扩展信道。

离散无记忆信道(X-Y)的N次扩展信道(X-Y)在k(k=1,2,…N)时刻的输出随机变量Yk,只与该时刻k的输入随机变量Xk有关,与k时刻之前的输入随机变量序列(X1X2…Xk-1)和输出随机变量序列(Y1Y2…Yk-1)无关。离散信道具有“无记忆”性。即

离散无记忆信道(X-Y)的N次扩展信道(X-Y)在时刻1,2,…,(k-1)的输出随机变量序列(Y1Y2…Yk-1),只与时刻1,2,…,(k-1)的输入随机变量序列X1X2…Xk-1有关,与下一时刻k(k=2,3,…,N)的输入随机变量序列Xk无关。离散无记忆信道具有“无预感”性。即

【例4.8】试写出二进制对称离散无记忆信道的N=2次扩展信道的数学模型

解:设二进制对称信道矩阵为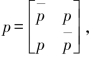令α1=00,α2=01,α3=10,α4=11;β1=00,β2=01,β3=10,β4=11。二次扩展信道输入为X=X1X2,输出Y=Y1Y2,(www.daowen.com)

X的取值为αi,i=1,2,3,4

Y的取值为βj,j=1,2,3,4

则二次扩展信道的信道矩阵为

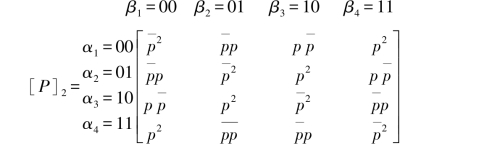
原信道及扩展信道的信道传递概率图,如图4.5和4.6所示。

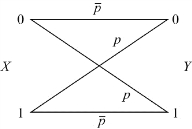
图4.5　原信道

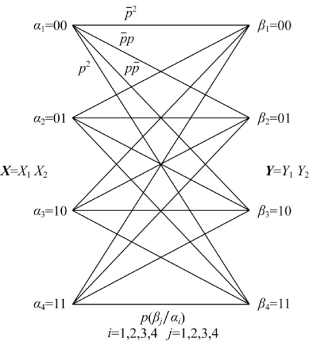
图4.6　扩展信道