一般情况下,信源输出的符号序列中符号之间的依赖关系是有限的,即任一时刻信源符号发生的概率仅与前面已经发出的若干个符号有关,而与更前面发出的符号无关。对于这种情况,我们可以视为信源在某一时刻发出的符号与信源所处的状态有关。设信源的状态空间为S={s1,s2,…,sJ},在每一个状态下信源可能输出的符号X∈A=(a1,a2,…,aq)。并认为每一时刻当信源发出一个符号后,信源所处的状态将发生变化,并转入一个新的状态。信源输出的随机符号序列为x1x2…xl…,xl∈A=(a1,a2,…,aq),l=1,2,…,信源所处的状态序列为u1u2…ul…,ul∈S=(S1,S2,…,SJ),l=1,2,…。
定义4.5.4 若信源输出的符号序列和状态序列满足下列条件则称此信源为马尔可夫信源。
1.某一时刻信源符号的输出只与当时的信源状态有关,而与以前的状态无关,即
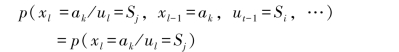
其中,ak∈A=(a1,a2,…,aq),Si,Sj∈S=(S1,S2,…,SJ)。
2.信源状态只由当前输出符号和前一时刻信源状态唯一确定,即
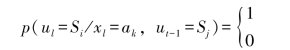
类似地,可以定义m阶马尔可夫信源。
定义4.5.4表明,信源输出的符号序列xl=ak,l=1,2,…完全由信源所处的状态ul=Sj决定。故可将信源输出的符号序列xl,l=1,2,…变换成信源状态序列ul,l=1,2,…。于是将一个讨论信源输出符号的不确定性问题变换成讨论信源状态转换的问题。从定义还可以看出,若信源在l-1时刻处于某一状态Sj,它是信源状态空间S中可能状态中的一个,当信源发出一个符号后,所处的状态就变了,从Sj状态变成Si状态,显然信源状态的转移依赖于信源发出的符号和所处的状态。状态之间的一步转移概率为
![]()
其中,Si,Sj∈S=(S1,S2,…,SJ)。它表示前一时刻(l-1)信源处于Sj状态下,在下一时刻l信源将处于Si状态。
马尔可夫信源在数学上可以用马尔可夫链来处理,因而可以用马尔可夫链的状态转移图来描述马尔可夫信源。
【例4.5】设有一个二进制一阶马尔可夫信源,其信源符号集为A=(0,1),条件概率为
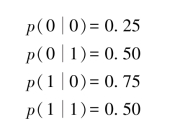
由于信源符号数q=2,因此二进制一阶信源仅有2个状态S1=0,S2=1。信源的状态图如图4.1所示。由条件概率求得信源转移概率为
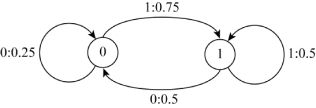
图4.1 一阶马尔可夫信源状态转移图
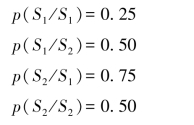
【例4.6】设有一个二进制二阶马尔可夫信源,其信源符号集为(0,1),条件概率为
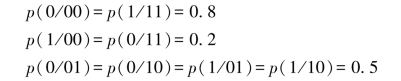
这个信源的符号数是q=2,故共有qm=22=4个可能的状态:S1=00,S2=01,S3=10,S4=11。如果信源原来所处的状态为S1=00,则下一个状态信源只可能发出0或1。故下一时刻只可能转移到00或01状态,而不会转移到10或11状态。同理还可以分析出初始状态为其他状态时的状态转移过程。由条件概率容易求得
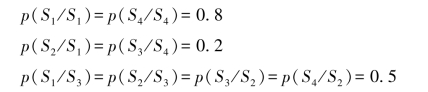
除此之外,其余为零。该信源的状态转移图如图4.2所示。
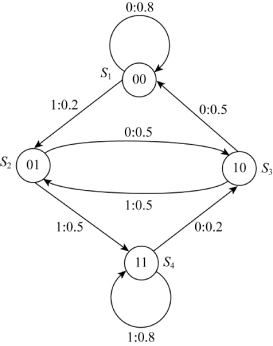
图4.2 二阶马尔可夫信源状态转移图
该信源的状态转移矩阵为

由此例看出,对于一般的m阶马尔可夫信源(https://www.daowen.com)
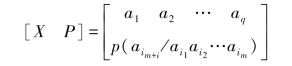
可通过引入状态转移概率,而转化为马尔可夫链,即令
![]()
从而得到马尔可夫信源状态空间
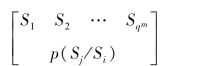
其中,状态转移概率p(Sj/Si)由信源符号条件概率
![]()
确定,其中i,j∈(1,2,…,qm)。
下面计算遍历的m阶马尔可夫信源所能提供的平均信息量,即信源的极限熵H∞。
由前面的分析可知,当时间足够长后,遍历的m阶马尔可夫信源可以视作平稳信源来处理。又因为信源发出的符号只与最近的m个符号有关,所以得
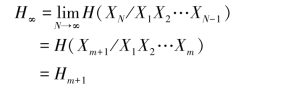
下面计算Hm+1。
对于齐次、遍历的马尔可夫链,其状态Sj由(ak 1,…,akm)唯一确定,因此有
![]()
上式两端同时取对数,并对(akm+1,akm,…,ak1)和Sj取统计平均,然后取负,得
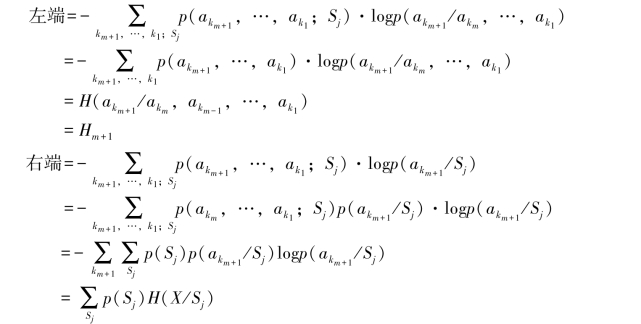
亦即
![]()
其中p(Sj)是马尔可夫链的平稳分布,它可以根据定理4.5.1给出的方法计算。熵函数H(X/Sj)表示信源处于某一状态Sj时发出一个消息符号的平均不确定性。
下面举例说明马尔可夫信源熵的计算方法。
【例4.7】考虑图4.2所示的二阶马尔可夫信源状态转移图。该信源的四个状态都是遍历的。于是,根据定理4.5.1可知,设W=[W1 W2 W3 W4]
其中,W1=p(S1),W2=p(S2),W3=p(S3),W4=p(S4)。
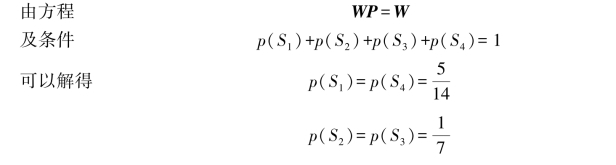
从而求得信源熵H∞,即
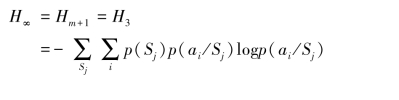
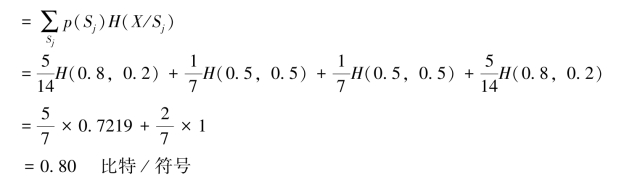
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








