定义4.5.1　设{Xn,n∈N+}为一随机序列,时间参数集N+={0,1,2,…},其状态空间S={s1,s2,…,sJ},若对所有n∈N+,有

则称{Xn,n∈N+}为马尔可夫链。

该式的直观意义是:系统在现在时刻n-1处于状态sin-1,那么将来时刻n的状态sin与过去时刻n-2,n-3,…,1的状态sin-2,…,si1无关,仅与现在时刻n-1的状态sin-1有关。简而言之,已知系统的现在,那么系统的将来与过去无关。这种特性称为马尔可夫特性。

在处理实际问题时,常常需要知道系统状态的转化情况,因此引入转移概率

转移概率pij(m,n)表示已知在时刻m系统处于状态si,或说Xm取值si的条件下,经(n-m)步后转移到状态sj的概率。也可以把pij(m,n)理解为已知在时刻m系统处于状态i的条件下,在时刻n系统处于j的条件概率,故转移概率实际上是一个条件概率。因此,转移概率具有下述性质:

(1)pij(m,n)≥0 i,j∈S

(2)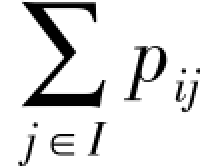(m,n)=1 j∈S

由于转移概率是一条件概率,因此第一个性质是显然的;对于第二个性质,有

我们特别关心n-m=1,即pij(m,m+1)的情况。把pij(m,m+1)记为pij(m),m≥0,并称为基本转移概率,有些地方也称它为一步转移概率。

括号中m表示转移概率与时刻m有关。显然,基本转移概率具有下述性质:

(1)pij(m)≥0 i,j∈S

(2)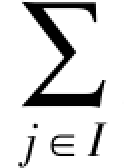pij(m)=1 i∈S

类似地,定义k步转移概率为

它表示在时刻m时,Xm的状态为i的条件下,经过k步转移到达状态j的概率。显然有:

当k=1时,它恰好是一步转移概率

通常还规定

由于系统在任一时刻可处于状态空间S={0,±1,±2,…}中的任意一个状态,因此,状态转移时,转移概率是一个矩阵

称为k步转移矩阵。由于所有具有性质1,2的矩阵都是随机矩阵,故式(4.4)也是一个随机矩阵。它决定了系统X1,X2,…,所取状态转移过程的概率法则。p(k)ij(m)对应于矩阵P中的第i行j列之元素。由于一般情况下,状态空间S={0,±1,±2,…}是一个可数无穷集合,所以转移矩阵P是一个无穷行无穷列的随机矩阵。

定义4.5.2　如果在马尔可夫链中

即从状态i转移到状态j的概率与m无关,则称这类马尔可夫链为时齐马尔可夫链,或齐次马尔可夫链。有时也说它是具有平稳转移概率的马尔可夫链。

对于时齐马尔可夫链,一步转移概率pij具有下述性质:

(1)pij≥0 i,j∈S

(2)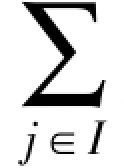pij=1 i∈S

由一步转移概率pij可以写出其转移矩阵为

或

显然矩阵P中的每一个元素都是非负的,并且每行之和均为1。如果马尔可夫链中状态空间S={0,1,2,…,n}是有限的,则称为有限状态的马尔可夫链;如果状态空间S={0,±1,±2,…}是无穷集合,则称它为可数无穷状态的马尔可夫链。

对于具有m+r步转移概率的齐次马尔可夫链,存在下述切普曼-柯尔莫哥洛夫方程

或写成

【证明】应用全概率公式可以证明上式成立

根据马尔可夫链特性及齐次性,可得上式中第一个因子为

而第二个因子为

将上述结果代入式(4.6)后,则式(4.5)得证。

利用方程式(4.5)就可以用一步转移概率表达多步转移概率。事实上,有(www.daowen.com)

一般地有

值得指出的是,转移概率pij不包含初始分布,亦即第0次随机试验中X0=Si的概率不能由转移概率pij表达。因此,还需引入初始分布。

定义4.5.3　若齐次马尔可夫链对一切i,j存在不依赖于i的极限

且满足

则称其具有遍历性,pj称为平稳分布。其中pi为该马尔可夫链的初始分布。

遍历性的直观意义是,不论质点从哪一个状态Si出发,当转移步数n足够大时,转移到状态Sj的概率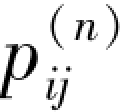都近似等于某个常数pj。反过来说,如果转移步数n充分大,就可以用常数pj作为n步转移概率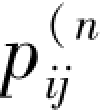)的近似值。这意味着马尔可夫信源在初始时刻可以处在任意状态,然后信源状态之间可以转移。经过足够长时间后,信源处于什么状态已经与初始状态无关。这时,每种状态出现的概率已经达到一种稳定分布,即平稳分布。

对于一个有r个状态的马尔可夫链,若令

则可以写出t=n-1与t=n时刻的状态方程

设

则式(4.7)可以表示成

将上式递推运算后可得

这就是说,t=n时刻的状态分布矢量W(n)是初始分布矢量W(0)与转移矩阵P的n次幂的乘积。对于有限状态马尔可夫链,如果存在一个数集W1,W2,…,Wr,且满足

则称该马尔可夫链的稳态分布存在。

关于有限状态马尔可夫链的存在性,详细证明可参阅有关文献。这里,我们给出两个定理。

定理4.2　设有一马尔可夫链,其状态转移矩阵为P=(pij),i,j=1,2,…,r,其稳态分布为Wj,j=1,2,…,r,则

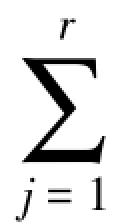1.Wj=1

2.W=(W1,W2,…,Wr)是该链的稳态分布矢量,即

进而,如果初始分布W0=W,则对所有的n,W(n)=W

3.W是该链的唯一稳态分布,即如果有

而且

则

这意味着

定理4.3　设P为某一马尔可夫链的状态转移矩阵,则该链稳态分布存在的充要条件是存在一个正整数N,使矩阵PN中的所有元素均大于零。

实质上,由上述定理所给定的条件等价于存在一个状态Sj和正整数N,使得从任意初始状态出发,经过N步转移之后,一定可以达到状态Sj。同时,从该定理中可以推出,如果P中没有零元素,即任一状态经一步转移后便可到达其他状态,则稳态分布存在。

【例4.4】设有一马尔可夫链,其状态转移矩阵为

为了验证它是否满足定理4.3的条件,我们计算矩阵

和矩阵

其中,星号“*”表示非零元素。因此,这个马尔可夫链是遍历的,其稳态分布存在。

由于WP=W

其中,W=(W1W2W3),即

由上式可以求解出