I(ai;bj)表示单个事件间的交互信息量,要求信道两端平均一对符号传递信息量的多少,就要计算平均交互信息量,如图3.8和图3.9所示。

图3.8　信息传输方向为X到Y

图3.9　信息传输方向为Y到X

首先给出两种特殊形式

1.

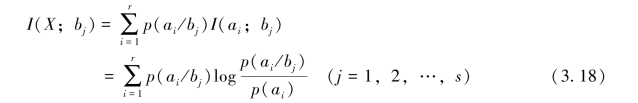
这表示信宿收到bj后,获得有关信源的信息量。

2.

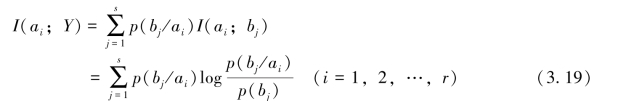
这表示反向信道中信宿收到ai后获得有关信源Y的信息量。

由上述两个式子可知,X与Y间平均传递一个符号所传输的平均信息量I(X;Y)应该是I(ai;bj)在联合集XY中的统计均值,即

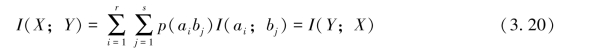
同样,I(X;Y)也有三种不同的表达形式

1.正向信道中收到Y前后关于X的不确定性的消除

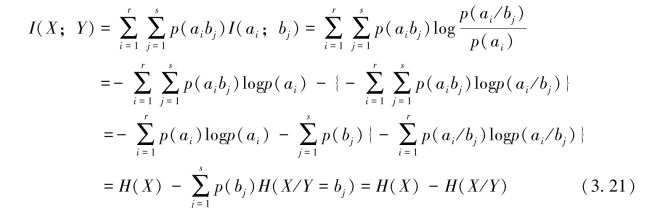
其中,

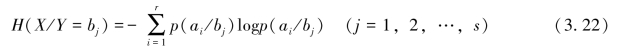
表示在随机变量Y=bj(j=1,2,…,s)的前提下,对随机变量X仍然存在的平均不确定性。而条件熵

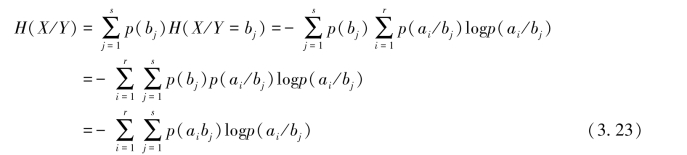
表示收到随机变量Y后,对随机变量X仍然存在的平均不确定性,通常称它为疑义度。

(3.21)式表明,从收到Y中获取关于X的平均交互信息量I(X;Y),等于收到Y前对X的平均不确定性H(X),与收到Y后对X仍然存在的平均不确定性H(X/Y)之差,即收到Y前、后,关于X的平均不确定性的消除。

2.反向信道中收到X前后关于Y的不确定性的消除

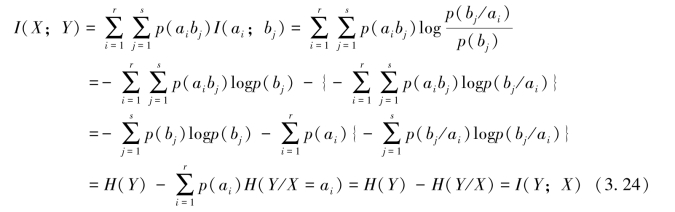
其中,

表示在随机变量X=ai(i=1,2,…,r)的前提下,随机变量Y仍然存在的平均不确定性。而条件熵

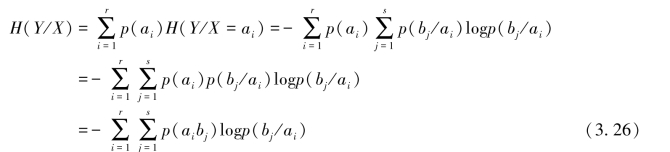
表示表示在反向信道中,收到随机变量X后,对随机变量Y仍然存在的平均不确定性。这个“反向疑义度”一般称为噪声熵。

式(3.24)表明,对于反向信道来说,从输出随机变量X中,获取关于Y的平均交互信息量I(Y;X),等于信宿收到X前,对Y的先验不确定性H(Y),与信宿收到X后,对Y仍然存在的后验平均不确定性H(Y/X)之差,即通信前、后,关于Y的平均不确定性的消除。

3.通信前后,随机变量X和Y同时出现的平均不确定性的消除

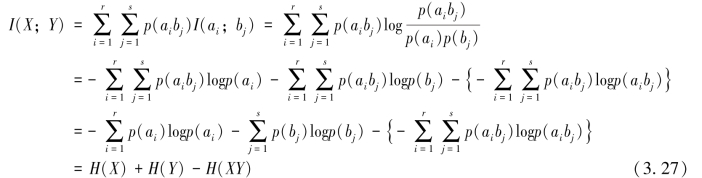
其中,

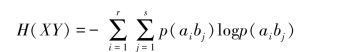
表示通信后,信道两端同时出现X和Y的后验平均不确定性,通常称它为共熵。(www.daowen.com)

式(3.27)表明,信源X通过传递概率为P(Y/X)的信道输出随机变量Y,信道传递的平均交互信息量I(Y;X),等于通信前(随机变量X和Y统计独立)随机变量X和Y同时出现的平均不确定性{H(X)+H(Y)},与通信后(随机变量X和Y由信道传递概率P(Y/X)相联系)信道两端同时出现随机变量X和Y的平均不确定性H(XY)之差,即通信前、后,随机变量X和Y同时出现的平均不确定性的消除。

上述讨论的通信系统中各类熵的关系可用维拉图形象表示,如图3.10所示。

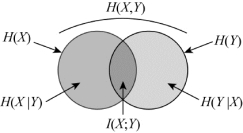
图3.10　通信系统中各类商关系图

【例3.6】设信源X的符号集X:{a1,a2},先验概率分布为p(a1)=ω(0＜ω＜1);p(a2)=1-ω。信道的输入符号集X:{a1,a2},输出符号集:Y:{a1,a2},传递概率P(Y/X):{p(aj/ai)=pij(i=1,2;j=1,2)}。现将信源X与如图3.11信道相接。

(一)试写出平均交互信息量I(X;Y)的一般表达式;

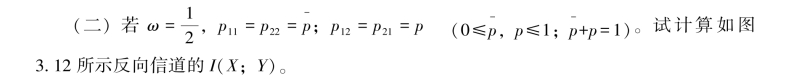
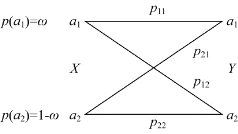
图3.11　正向信道传递概率图

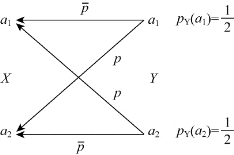
图3.12　反向信道传递概率图

解:(一)平均交互信息量I(X;Y)的一般表达式

(1)各联合概率

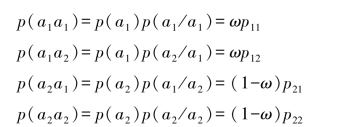
(2)随机变量Y的概率分布

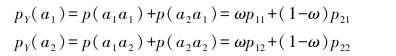
(3)求随机变量Y的熵

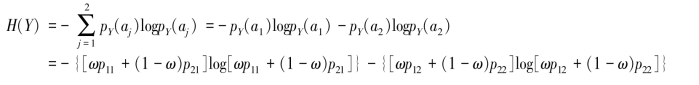
(4)由p(aj/ai)=pij(i=1,2;j=1,2)求得条件熵

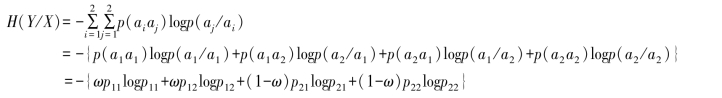
(5)求得平均交互信息量

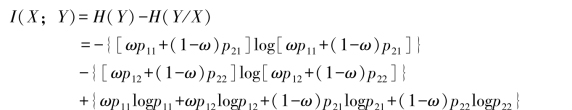
这说明平均交互信息量是信源概率分布ω和信道传递概率pij(i=1,2;j=1,2)的函数。

(二)计算反向信道的I(X;Y)

(1)各联合概率

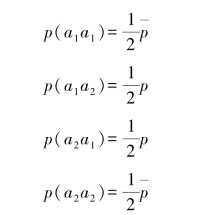
(2)随机变量Y的概率分布

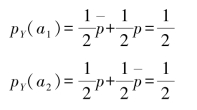
(3)求随机变量Y的熵

(4)由p(aj/ai)=pij(i=1,2;j=1,2),求得噪声熵

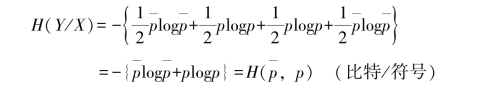
(5)求得平均交互信息量