现在把目光转到级联信道的交互信息的讨论上。

如图3.7所示信道I与信道II串接。信道I的输入符号集X={a1,a2,…,ar},输出符号集Y={b1,b2,…,bs},信道II的输入符号集Y={b1,b2,…,bs},输出符号集Z={c1,c2,…,ct}

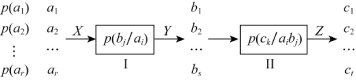
图3.7　信道Ⅰ与信道Ⅱ串接

信道I的传递概率:

信道II的传递概率:

则p(aibjck)=p(ai)p(bj/ai)p(ck/aibj)(i=1,2,…,r;j=1,2,…,s;k=1,2,…,t)由X、Y、Z的联合概率p(aibjck)可以求得其他各种概率分布。

一维分布:

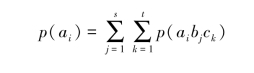
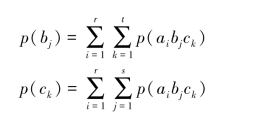
二维分布:

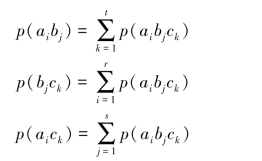
进一步求得条件概率分布:

在串接信道输出某符号ck条件下,从符号bj中获取符号ai的信息量定义为

该式表明,ck已知条件下,bj出现前后对ai的条件不确定性的消除。

用p(bjck)同时乘上式右边的分子、分母,则有

上式表明,I信道通信前、后,输入输出端同时出现ai和bj的条件不确定性的消除。由3.17式,做进一步变换,有

所以有I(ai;bj/ck)=I(bj;ai/ck)

在图3.7中,随机变量ck与随机变量X和Y的联合符号(aibj)之间的相关交互信息量

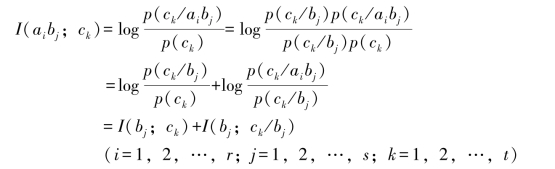
这表明,相关交互信息量I(aibj;ck)等于bj与ck之间的交互信息量I(bj;ck),再加上bj已知的条件下,ai与ck之间的条件交互信息量I(ai;ck/bj)所得之和。同样(www.daowen.com)

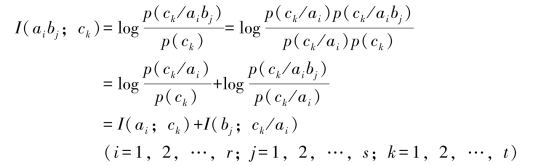
这表明,相关交互信息量I(aibj;ck)也等于ai与ck之间的交互信息量I(ai;ck),再加上ai已知的条件下,bj与ck之间的条件交互信息量I(bj;ck/ai)所得之和。

【例3.5】如表3.1所示,列出了无失真信源编码的信源消息、消息的先验概率以及每一个消息所对应的码字。

表3.1　信源输出符号的条件概率

试以消息a5及相应码字(100)为例,分别说明码字(100)中每一个码符号对消息a5提供的信息量。

解:根据相关交互信息量的理论可有

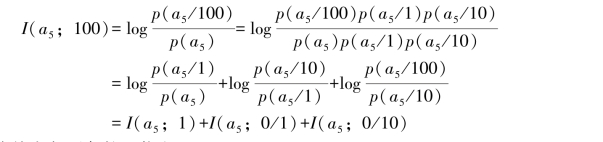
以下分别计算其中各项条件互信息。

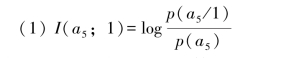
其中,p(a5/1)表示收到码符号“1”后,判断信源发消息a5的后验概率。因为收到码符号“1”后,再收到码符号序列“00”就构成码字(100),即消息a5出现。所以后验概率p(a5/1)=p(00/1),即有

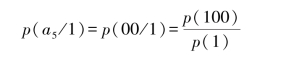
其中,码字(100)出现的概率p(100)等于消息a5出现的概率,即有p(100)=p(a5)=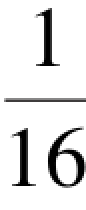

从表3.1中可看出,8个码字中有4个码字(100)、(101)、(110)、(111)的第一个码符号是“1”,所以有

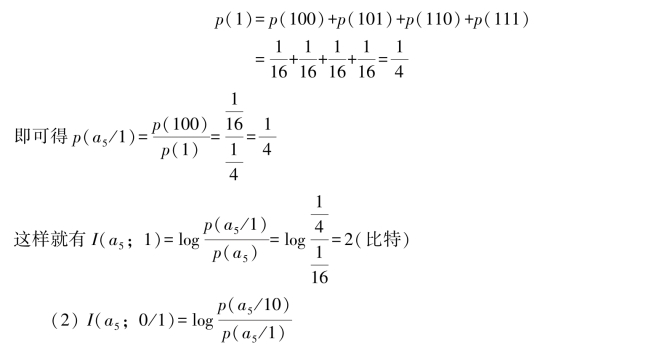
其中,p(a5/10)表示收到码符号“10”后,判断信源发消息a5的后验概率。因为收到码符号“10”后,再收到码符号序列“0”就构成码字(100),即消息a5出现。所以后验概率p(a5/10)=p(0/10),即有p(a5/10)=p(0/10)=

从表3.1中可看出,8个码字中有2个码字(100)、(101)的前两个码符号序列是“10”,所以有

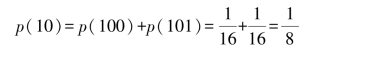
其中,p(a5/100)表示收到码符字(100)后,判断信源发消息a5的后验概率。显然收到(100)后也就是收到了消息a5,所以有p(a5/100)=1

以上三项计算结果表明,在消息a5相对应的码字(100)中:第一个码符号“1”提供关于消息a5的信息量I(1;a5)=I(a5;1)=2(比特);在收到第一个码符号“1”的条件下,第二个码符号“0”提供关于a5的条件交互信息量I(0;a5/1)=I(a5;0/1)=1(比特);在收到第一个码符号“1”和第二个码符号“0”组成的码符号序列“10”的条件下,第三个码符号“0”提供关于a5的条件交互信息量I(0;a5/10)=I(a5;0/10)=1(比特)。所以,从码字(100)中的三个码符号总共提供关于消息a5的相关交互信息量

另一方面,消息a5的自信息量

这从信息测量的角度证实了由于消息a5与相应的码字(100)是一一对应的确定关系,相关交互信息量I(a5;100)就是消息a5的自信息量I(a5)。