在求解信道输入输出单个符号对应互信息量前,先讨论信道输入输出变量的统计特性。通信系统模型如图3.5所示

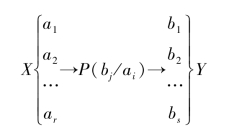
图3.5　系统模型

为方便讨论,首先定义几种概率的名称。

1.先验概率

信源X输出符号ai的概率p(x=ai)=p(ai)(i=1,2,…,r)称为先验概率。

2.正向转移概率

从信道输入符号ai到信道输出符号bj的条件概率

称为正向转移概率。

3.后验概率

从信道输出符号bj到输出符号ai的条件概率

称为后验概率,又称之为反向转移概率。

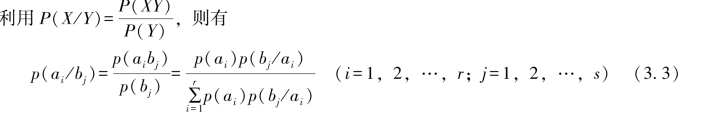
看到,已知先验概率和信道转移概率、后验概率即为确定。

4.联合概率

信源符号ai和信道输出符号bj的联合概率

由信源概率和信道转移概率唯一确定。

类似信道转移概率矩阵可以写出联合概率矩阵,也是r行s列矩阵。

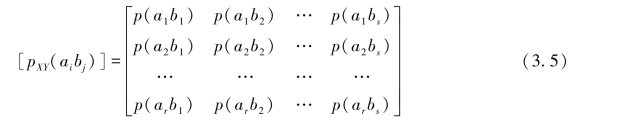
5.信宿概率

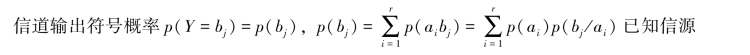
现在转入互信息量的讨论。

在通信系统中,信源发出某符号ai,由于受到噪声的随机干扰,在信道的输出端输出符号ai的某种变型bj,按信息的定义,信宿收到bj后,从bj中获取关于ai的信息量I(ai;bj),等于信宿收到bj前、后,对符号ai的不确定性的消除,即有

信宿收到bj前,对信源发符号ai的先验不确定性

信宿收到bj后,对信源发出的符号ai的后验不确定性

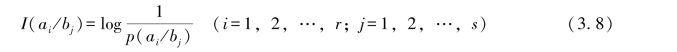
则可得互信息为

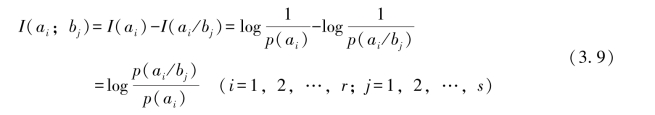
信宿收到bj后,从bj中获取关于的信息量I(ai;bj)称为输入符号ai和输出符号bj之间的交互信息量,简称为互信息。它表示信道在把输入符号ai传递为输出符号bj的过程中,信道所传递的信息量。(3.9)式称为符号ai和bj之间的互信息函数。

现在就互信息量表达式所代表的物理含义做进一步说明。

1.当p(ai/bj)=1时,有

(www.daowen.com)

p(ai/bj)=1表明收到的bj(j=1,2,…,s)后,即可确切无误地判断发端符号为ai,消除对ai的全部不确定性,收端获得关于ai的全部信息量I(ai)(i=1,2,…,r)。

2.当p(ai)＜p(ai/bj)＜1时,有

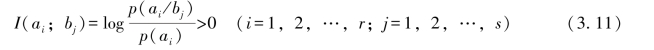
这就意味着,收信者收到bj后,判断信源发ai(i=1,2,…,r)的可能性,比对于收到bj(j=1,2,…,s)前判断信源发ai(i=1,2,…,r)的可能性更大;也就是说收到bj(j=1,2,…,s)后对信源发ai(i=1,2,…,r)的不确定性,比收到bj(j=1,2,…,s)前有所减小,收信者从bj(j=1,2,…,s)中就可获取关于ai(i=1,2,…,r)的一定信息量。

3.当p(ai/bj)=p(ai)时,有

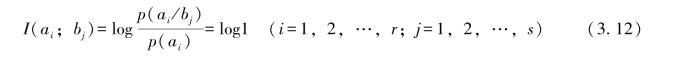
由p(aibj)=p(ai)p(bj/ai)=p(ai)p(bj)得到,符号ai与符号bj统计独立。

说明,收信者收到bj(j=1,2,…,s)前、后,判断信源发ai(i=1,2,…,r)的可能性大小没有任何变化,收信者在收到bj(j=1,2,…,s)前、后,对判断信源发ai(i=1,2,…,r)的不确定性没有任何减小,收信者从bj(j=1,2,…,s)中得不到关于ai(i=1,2,…,r)的任何信息量。

4.当0＜p(ai/bj)＜p(ai)时,有

式(3.13)表明,由于信道噪声的干扰,收到符号bj(j=1,2,…,s)后,猜测符号ai(i=1,2,…,r)的难度反而加大。

互信息量I(ai;bj)的另外两种表达形式

1.第一种表达形式

2.第二种表达形式

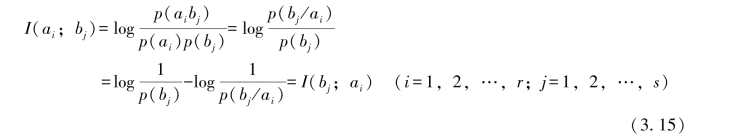
ai→bj,构成正向信道;

bj→ai,构成反向信道。

说明在反向信道中,从ai中获得关于bj的信息量等于在正向信道中从bj中获得关于ai的信息量,即I(ai;bj)=I(bj;ai)。

【例3.3】二元删除信道,简记为BEC(Binary Erasure Channel):其中输入符号集A={a0,a1}={0,1},输出符号集B={b0,b1,b2}={0,2,1},p(a0)=p(a1)=0.5,写出信道的转移概率矩阵及互信息量I(ai;bj)。

解:设信道的转移概率矩阵为

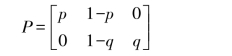
联合概率为

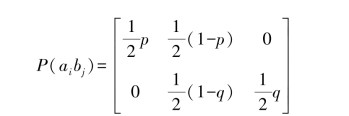
则P(bj)为

那么互信息量I(ai;bj)用矩阵形式简写为

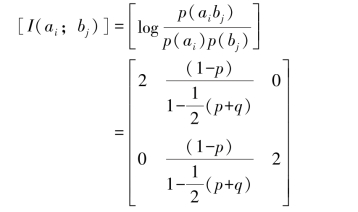
【例3.4】4个等概率消息,编程的码字为M1=000,M2=011,M3=101,M4=110,通过如图3.6所示二元对称无记忆信道(ε＜0.5)传输,求:(1)事件“接收到第一个数字为0”与发送M1之间的互信息;(2)当接收到第二个数字也为0时,关于M1的附加信息;(3)当接收到第三个数字也为0时,又增加了多少关于M1的信息?

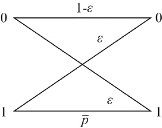
图3.6　二元对称无记忆信道

解:记“0”表示第一个接收数字为0,“00”表示第一、二个接收数字都为0,“000”表示前三个接收数字都为0;q(·)表示接收符号的概率;p(y/x)为信道的转移概率。

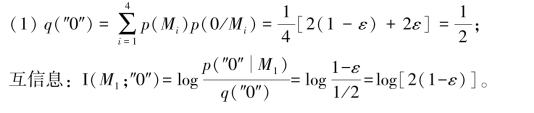
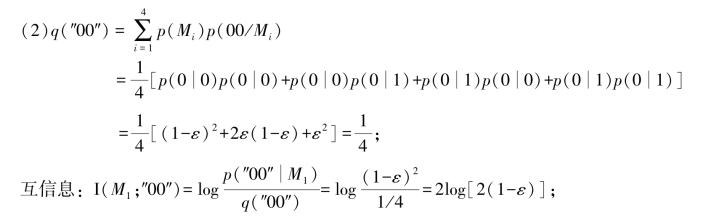
附加信息:log[2(1-ε)]

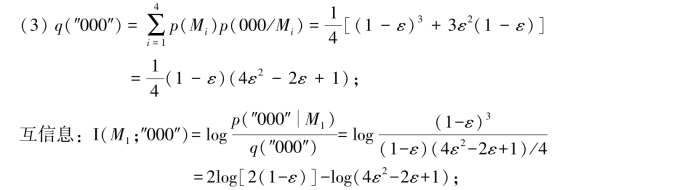
又增加的信息为-log(4ε2-2ε+1)