【摘要】：图3.1单符号离散信道模型输入变量X有r种取值,即输入符号集X:{a1,a2,…,r),表明信道矩阵行和是1。信道特性也可以形象、直观地用信道转移图表示图3.2信道转移图二进制对称信道,简记为BSC,输入输出符号集分别为X:{0,1},Y:{0,1},信道转移概率满足PY/X(0/0)=PY/X(1/1)=1-p,PY/X(1/0)=PY/X(0/1)=p,p为错误传输概率。图3.3二进制对称信道转移概率图二进制删除信道,简记为BEC其中输入集X:{0,1},输出集Y:{0,2,1},转移概率如图3.4所示。图3.4二进制删除信道转移概率图写出信道的转移概率矩阵。
单符号离散信道模型如图3.1所示。
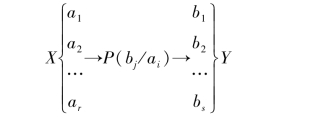
图3.1 单符号离散信道模型
输入变量X有r种取值,即输入符号集X:{a1,a2,…,ar},输出变量Y有s种取值,即输出符号集{b1,b2,…,bs}。信道转移概率
共有r×s个取值,体现了信道的符号传递特性。
写成矩阵形式,形成一个(r×s)阶矩阵,矩阵行数代表信道输入符号个数,矩阵列数代表输出符号个数。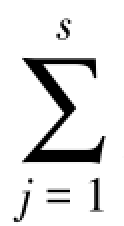
p(bj/ai)=1(i=1,2,…,r),表明信道矩阵行和是1。信道特性也可以形象、直观地用信道转移图表示
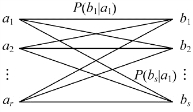
图3.2 信道转移图(www.daowen.com)
【例3.1】二进制对称信道,简记为BSC(Binary Semmetric Channel),输入输出符号集分别为X:{0,1},Y:{0,1},信道转移概率满足PY/X(0/0)=PY/X(1/1)=1-p,PY/X(1/0)=PY/X(0/1)=p,p为错误传输概率。写出信道的转移概率矩阵,并画出转移概率图。
解:转移概率矩阵为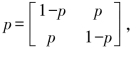
相应的信道转移概率矩阵如图3.3所示。
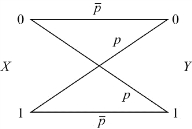
图3.3 二进制对称信道转移概率图
【例3.2】二进制删除信道,简记为BEC(Binary Erasure Channel)其中输入集X:{0,1},输出集Y:{0,2,1},转移概率如图3.4所示。
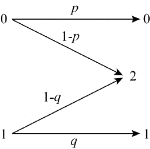
图3.4 二进制删除信道转移概率图
写出信道的转移概率矩阵。
解:信道的转移概率矩阵为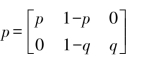
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
