1.对称性

概率矢量p=(p1,p2,…,pn)中,各分量的次序任意改变,熵不变,即

其中,j1,j2,…,jn是1,2,…,n的任何一种n级排列。该性质说明熵仅与随机变量总体概率特性(即概率分布)有关,而与随机变量的取值及符号排列顺序无关。

2.非负性

仅当对某个pi=1时,等式成立。

因为自信息量是非负的,熵为自信息的平均,所以也是非负的。不过,非负性仅对离散熵有效,而对连续熵来说这一性质并不成立。

3.确定性

这就是说,当随机变量集合中任一事件概率为1时,熵就为0。这个性质意味着,从总体来看,事件集合中虽含有许多事件,但是如果只有一个事件几乎必然出现,而其他事件几乎都不出现,那么,这就是一个确知的变量,其不确定性为0。

4.扩展性

利用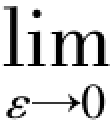εlogε=0可得到上面的结果,其含义是,虽然小概率事件自信息量大,但在计算熵时所占比重很小,可以忽略。

5.极值性

定理2.5(离散最大熵定理)　对于有限离散随机变量,当符号集中的符号等概率发生时,熵达到最大值。

【证明】设随机变量有n个符号,概率分布为P(x);Q(x)为等概率分布,即Q(x)=1/n。根据散度不等式有

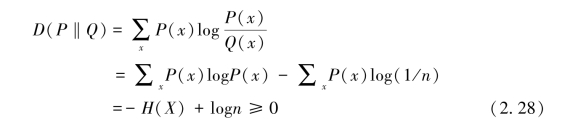
即,仅当P(x)等概布时等号成立。

注意:离散最大熵定理仅适用于有限离散随机变量,对于无限可数符号集,只有附加其他约束求最大熵才有意义。

6.上凸性

H(p)=H(p1,p2,…,pn)是概率矢量p的严格的上凸函数。(www.daowen.com)

这就是说,若p=θp1+(1-θ)p2,那么H(p)＞θH(p1)+(1-θ)H(p2),其中p,p1,p2均为n维概率矢量,0≤θ≤1。该性质可用凸函数性质(1)来证明(提示:先证明-pilogpi是严格上凸的)。

7.一一对应变换下的不变性

离散随机变量的变换包含两种含义,一是符号集中符号到符号的映射,二是符号序列到序列的变换。首先研究第一种情况。设两随机变量X,Y,符号集分别为A,B,其中Y是X的映射,可以表示为A→B,x→f(x)。因此有

所以H(Y/X)=0;H(XY)=H(X)+H(Y/X)=H(X),而另一方面H(XY)=H(Y)+H(X/Y)≥H(Y),所以H(X)≥H(Y),仅当f是一一对应映射时等号成立,此时H(X/Y)=0。应用类似的论证也可推广到多维随机矢量的情况,因此得到如下定理。

定理2.6　离散随机变量(或矢量)经符号映射后的熵不大于原来的熵,仅当一一对应映射时熵不变。

【例2.9】设二维随机矢量XY,其中X,Y为独立同分布随机变量,符号集为A={0,1,2},对应的概率为{1/3,1/3,1/3},做变换u=x+y,v=x-y,得到二维随机矢量UV;求H(U),H(V),H(UV)。

解:U,V取值空间如表2.1、表2.2所示。

表2.1　U取值

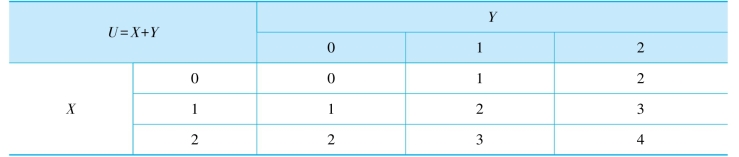
U的符号集为{0,1,2,3,4}

表2　V取值

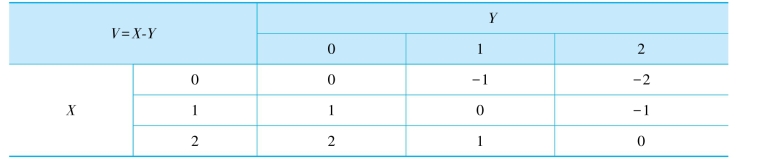
V的符号集为{-2,-1,0,1,2}

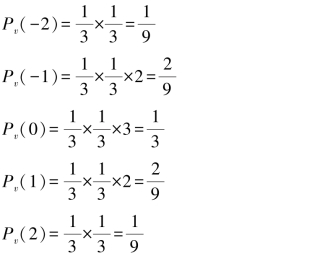
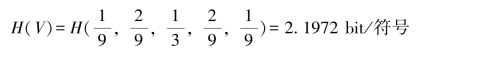
因为是一一对应变换,所以

H(UV)=H(XY)=H(X)+H(Y)=2log3=3.1699 bit/2个符号

看到H(UV)＜H(U)+H(V),所以U,V不独立。