自信息量I(ai)是针对具体的特定事件ai在发生前存在的不确定度的度量,或发生后,提供给接收者的信息量。自信量的度量具有个体差异性,不具备对信源总体不确定度的度量能力。对信源X总体进行信息度量,即信源熵,它表征信源平均每个符号所含有的不确定性或平均输出一个符号提供给观测者的信息量,是自信息量的统计均值,即有

熵的单位即自信息量的单位,取决于对数的底。

【例2.5】(a)设有一信源X由两个事件a1,a2组成,其概率空间如下

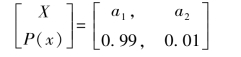
则其信源熵为

(b)设有另一信源Y如下

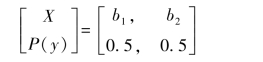
则

可见有H(Y)＞H(X),即信源Y的平均不确定性要大于信源X的平均不确定性。直观地分析也易得出这样一个结论:信源中各事件的出现概率越接近,则事先猜测某一事件发生的把握性越小,即不确定性越大。从后述信息熵的极值性质,我们可知:当信源各事件等概率出现时具有最大的信源熵,也即信源的平均不确定性最大。

【例2.6】设二元信源X的信源空间为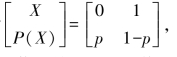其中,0≤p≤1。

(1)试计算当p=1/2;p=0(或p=1)时信息熵H(X)的值;

(2)信息熵H(X)是概率分量p的函数H(p)。画出H(p)的函数曲线,并指明函数H(p)的特性。

解:信源X的信息熵

这表明,二元信源X的信息熵H(X)是概率分量p的函数。

(1)当p=(1-p)=1/2时,二元信源X称为二维等概信源,其信息熵

这表明,二元等概信源X,每一个符号(不论是“0”还是“1”)含有的平均信息量是1比特,每发一个符号(不论是“0”还是“1”)提供的平均信息量是1比特;每一个符号(不论是“0”还是“1”)存在的平均不确定性是1比特;收信者能确切无误的收到信源X的“0”或“1”时,收信者每收到信源X的一个符号,获取的平均信息量是1比特。

(2)当p=0(p=1)时,二元信源X是一个确知信源,其信息熵

因为,对任意小的正数ε＞0,以“e”为底的对数lnε可展开成级数

当ε→0时,εlnε的极限值等于零,即有

所以

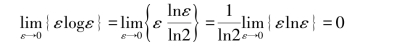
这样,可合理的约定

则当p=0(p=1)时,信源X的信息熵(www.daowen.com)

这表明,以概率1发符号“0”或“1”的二元确知信源,不存在任何不确定性,不含有任何信息量。

(3)当0＜p＜1时,取不同的p值,可计算出二元信源X的信息熵

相应地,得到H(p)函数曲线如图2.2所示

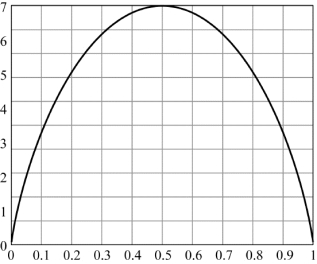
图2.2　H(p)函数曲线

从图中可见,若二元信源X发符号“0”(或“1”)是确定事件,即p=1(p=0)时,则H(p)=H(1)(或H(0))=0。这意味着确知信源X不提供任何信息量;若二元信源X以相同概率0.5发符号“0”或“1”,即p=1/2时,H(p)=1比特/信源符号。这意味着等概信源X每发一个符号提供的平均信息量达到最大值1比特/信源符号。若二元信源X发“0”(或“1”)的概率p(0＜p＜1)越接近1/2,则发“1”(或“0”)的概率(1-p)亦越接近1/2。若“0”和“1”的概率越接近则H(p)的值越大。这意味着二元信源X的平均不确定性越大,每符号(不论是“0”还是“1”)含有的平均信息量越大;相反,二元信源X发“0”(或“1”)的概率p(0＜p＜1)越远离1/2,则发“1”(或“0”)的概率(1-p)亦越远离1/2.若发“0”和“1”的概率相差越大,则H(p)的值就越小。这意味着二元信源X的平均不确定性越小,每符号(不论是“0”还是“1”)含有的平均信息量就越小。这体现出H(p)是概率分量p的上凸形函数的基本特性。

【例2.7】在一个箱子中装有m个黑球和(n-m)个白球。设实验X:随机的从箱子中取出一个球而不再放回箱子;实验Y:从箱子中取出第二个球。

(1)计算实验X所获取的平均信息量。

(2)若实验X摸取的第一个球的颜色不知道,计算实验Y所获取的平均信息量。

解:令W代表白球;B代表黑球。

(1)设实验X中取出的球是黑球的概率为PX(B);实验X中取出的球是白球的概率为PX(W),则有

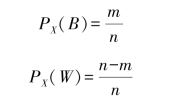
信源X的信源空间可表示为

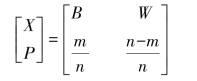
实验X所获取的平均信息量,就是信源X的信息熵

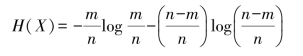
(2)若实验X中取出的第一个球是白球,令实验Y中取出的白球的概率为PY(W/W);取出黑球的概率为PY(B/W),则有

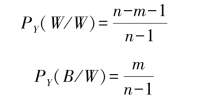
若实验X中取出的第一个球是黑球,令实验Y中取出白球的概率为PY(W/B);取出黑球的概率为PY(B/B),则有

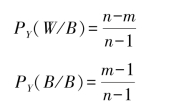
设实验Y中出现白球的概率为PY(W);出现黑球的概率为PY(B),则有

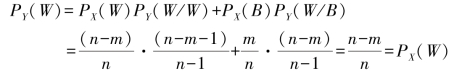
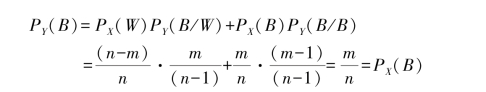
信源Y的信源空间可表示为

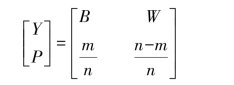
实验Y所获取的平均信息量,就是信源Y的信息熵

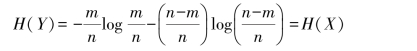
这说明,实验X和实验Y的平均不确定性或获取的平均信息量是相等的。