设信源发出某符号ai,由于信道中存在噪声或其他干扰,收端收到的是ai的某种变型bj,收信者收到bj后,从bj中获取关于ai的信息量,用I(ai;bj)表示,则

若信道是无噪无损信道,即一一对应信道,收信者收到bj就是ai本身,那么就完全消除了对信源符号ai的不确定性,即

把I(ai;ai)定义为信源符号ai的自信息量,并用I(ai)表示,即

信源符号的自信息量度量问题,相当于信源发符号的不确定性度量问题,是先验概率的函数:

根据自信息量定义所需的4个公理性条件,自信息量函数I(ai)定义如下:

自信息量I(ai)随p(ai)变化的曲线如图2.1所示。

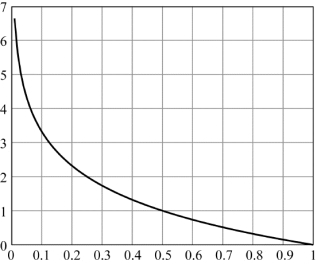
图2.1　自信息量I(ai)随p(ai)变化的曲线

自信息量的单位与对数的底有关

若以“2”为底,自信息量单位为“比特”(bit-binary unit),即

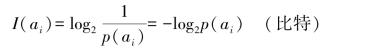
若以“e”为底,自信息量单位为“奈特”(nat-nature unit),即(www.daowen.com)

若以“10”为底,自信息量单位为“哈特”(Hart-Hartley),即

若以正整数“r”为底,自信息量单位为“r进制信息单位”,即

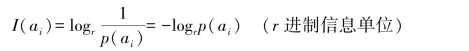
不同信息单位之间可以进行换算。本书如不加说明,信息度量默认为以“2”为底,且略去底数“2”不写。

香农信息量的度量,是信息论发展史上的里程碑,奠定了信息论发展成为一门学科的基础。

【例2.3】箱中80个红球,20个白球,现从箱中随机取出两个球。求:

(1)求解“两个球中红、白各一个”的不确定性;

(2)求解“两个球都是白球”所提供的信息量;

(3)求解“两个球都是白球”和“两个球都是红球”相比较,哪个事件发生的更难测?

解:设x为红球数,y为白球数,则

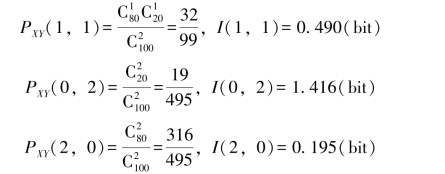
从上述计算结果来看,1.416bit大于0.195bit,显然,事件“两个球都是白球”要比事件“两个球都是红球”更难测。

【例2.4】设二元随机矢量XN=(X1,X2,…,XN),矢量中每个变量Xi(i=1,2,…,N)为独立同分布随机变量,且0符号的概率ω(0≤ω≤1)。求序列x=101100100的自信息量。

解:I(x)=-logp(x)=-logω4(1-ω)5=-4logω-5log(1-ω)