本实例通过弹簧阻尼-质量系统（见图9-7所示）介绍MotionView＆MotionSolve中的微分方程、线性系统方程和传递函数的建模方法。

弹簧阻尼-质量系统的动力学方程可写为

mx＆＆+cx＆+kx-f=0 （9-4）式中，x为方块位移，m为方块质量，k为弹簧刚度，c为弹簧阻尼，f为方块承受的重力。本例取m=1kg，k=10N/m，c=2Ns/m，f=10N，则弹簧阻尼-质量系统动力学方程可写为

x＆＆+2x＆+10x-10=0 （9-5）

将弹簧阻尼-质量系统动力学方程进行拉普拉斯变换，可得到弹簧阻尼-系统的传递函数为

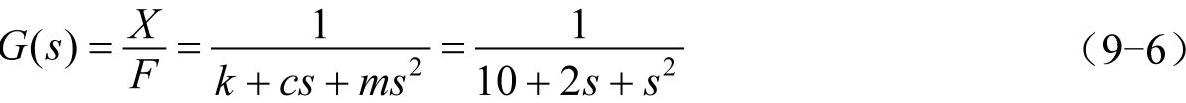
根据线性系统理论，

取x₁和x₂=x＆1为线性系统的状态变量，可将弹簧阻尼-质量系统动力学方程转化为线性系统方程：

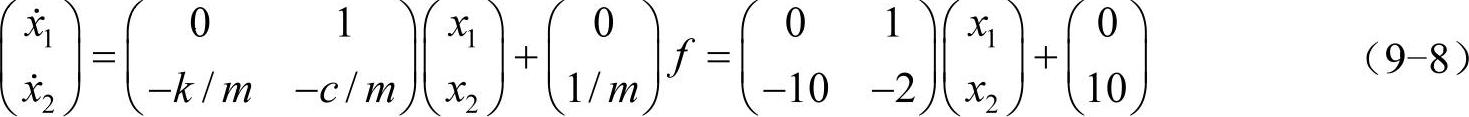
下面分别用微分方程、传递函数和线性系统方程方法进行弹簧阻尼-质量系统动力学分析。

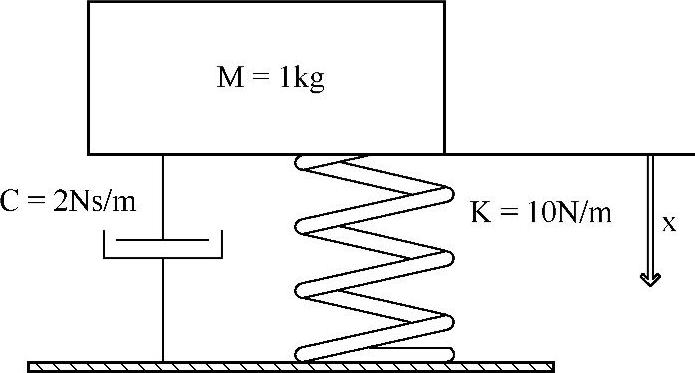
图9-7 弹簧阻尼-质量系统

1.微分方程方法

首先定义弹簧阻尼-质量系统数学模型。MotionView＆MotionSolve支持一阶微分方程的建模与求解，因此需将上述二阶微分方程降阶。另外，取状态变量初始值为x₁（0）=0，x₂（0）=0，由此得到的系统数学模型为：

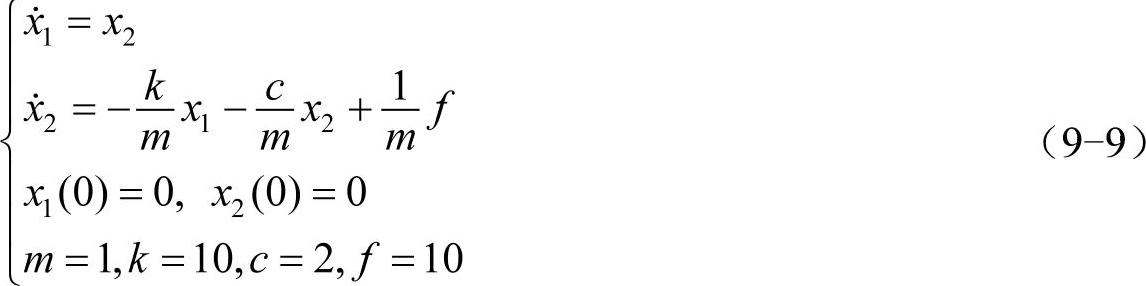
STEP 01 创建求解器变量

（1）启动MotionView，新建一个会话。

（2）从项目浏览树中右击Model，并选择Add Control Entity→Solver Variable（或右击工具栏中的“求解器变量”按钮）。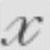

（3）在弹出的Add Solver Variable对话框中，指定标题为m。

（4）使用默认的变量名，如图9-8所示。

（5）单击OK按钮。

（6）在Solver Variable面板的Properties标签中，选择变量类型为Linear，并指定数值为1.0，如图9-9所示。

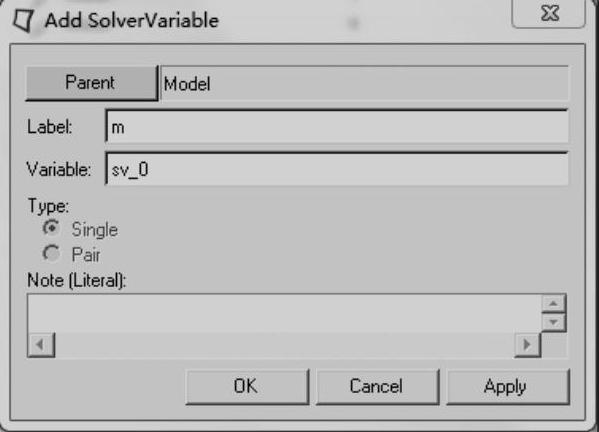
图9-8 Add Solver Variable对话框

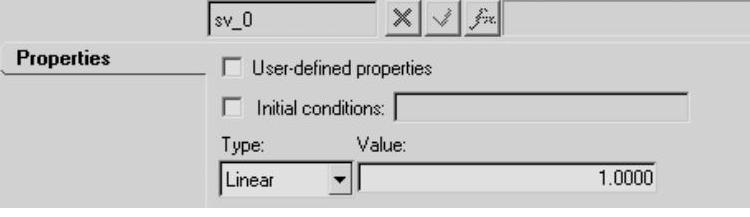
图9-9 Solver Variable面板

（7）重复上述步骤，分别定义系统变量k=10、c=2、f=10。

STEP 02 定义微分方程

（1）从项目浏览树中右击Model，并选择Add Control Entity→Solver Differential Equation（或右击工具栏中的“求解器变量”按钮）。

（2）在弹出的Add SolverDiff对话框中，指定标题为x1。

（3）使用默认的变量名，如图9-10所示。

（4）单击OK按钮。

（5）创建一个标题为x2的微分方程，变量名可取默认值。

（6）在项目浏览树中单击x1，进入微分方程面板。

（7）将微分方程类型设置为Value Expression，如图9-11所示。

（8）单击按钮，进入表达式编辑器对话框。

图9-10 Add SolverDiff对话框

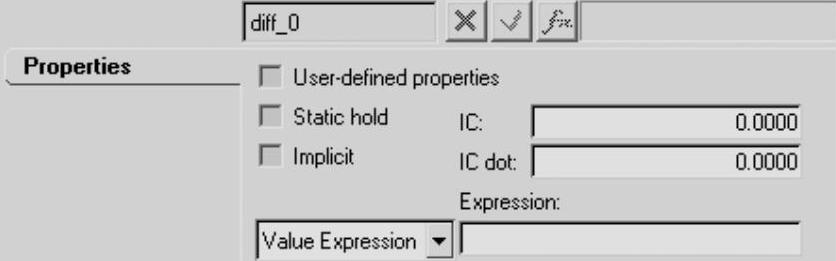
图9-11 Solver Differential Equation面板

（9）根据图9-12，创建微分方程`DIF（{diff_1.id}）`。创建完毕可单击Evaluated按钮对表达式进行评估。

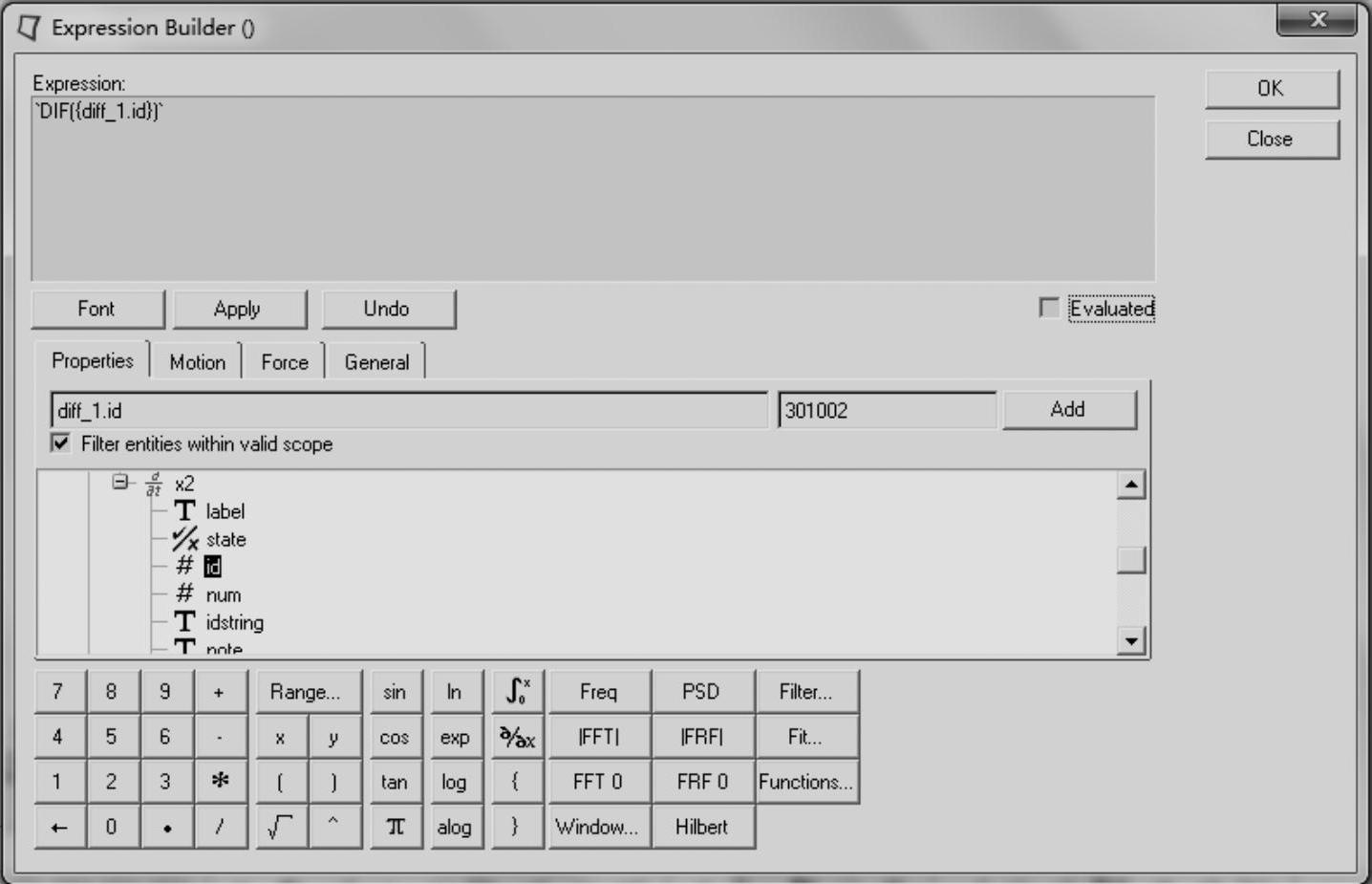
图9-12 表达式编辑器对话框

（10）单击OK按钮，微分表达式出现在微分方程面板中。

（11）重复步骤（6）～（10），创建第二个微分方程，表达式为 `-{sv_1.value.lin}/{sv_0.value.lin}*DIF（{diff_0.id}）-{sv_2.value.lin}/{sv_0.value.lin}*DIF（{diff_1.id}）+{sv_3.value.lin}/{sv_0.value.lin}`

STEP 03 定义输出

（1）右击工具栏中的Output按钮。

（2）在弹出的Add Output对话框中使用默认的标题与变量名创建一个输出请求。

（3）在Output面板中将输出请求类型设置为Expressions。

（4）激活F2，单击按钮，进入表达式编辑器对话框。

（5）定义输出请求表达式为`DIF（{diff_0.id}）`。此表达式将输出x1状态。

STEP 04 求解微分方程

（1）单击Save按钮 ，保存模型为Spring_Diff.mdl。

（2）单击工具栏中的Run按钮，进入Run面板。

（3）进入Simulation Parameter标签，将End time设置为5，其余使用默认设置。

（4）返回Main标签，单击“文件浏览”按钮。

（5）指定工作文件夹，将模型保存为Spring_Diff.xml。

（6）单击Run按钮，求解模型。

2.传递函数方法

STEP 01 定义单入单出传递函数

（1）启动MotionView，新建一个会话。

（2）从项目浏览树中右击Model，并选择Add Control Entity→ControlSISO（或右击工具栏中的“单入单出传递函数”按钮）。

（3）在弹出的Add ControlSISO对话框中，使用默认的标题和变量名新建一个传递函数。

（4）进入ControlSISO面板。

（5）激活Properties标签，定义传递函数参数，如图9-13所示。创建分母时，单击

Append按钮可增加项目。

图9-13 ControlSISO面板（Properties标签）

这里定义传递函数为

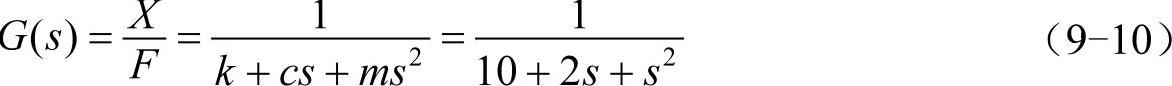
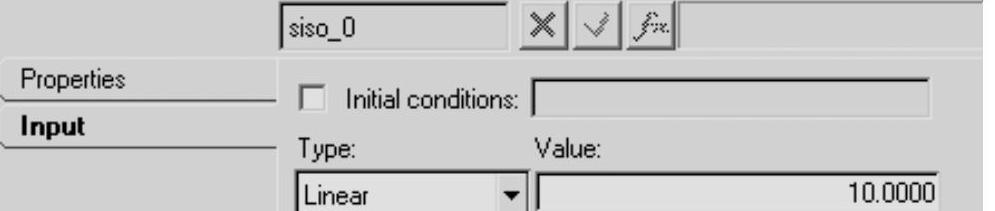
（6）进入Input标签，定义输入类型为Linear。

（7）指定输入值为10，如图9-14所示。

(www.daowen.com)

图9-14 ControlSISO面板（Input标签）

这里定义系统承受外载为10N。

STEP 02 定义输出

（1）右击工具栏中的Output按钮。

（2）在弹出的Add Output对话框中使用默认的标题与变量名创建一个输出。

（3）在Output面板中将输出请求类型设置为Expression。

（4）激活F2，单击按钮，进入表达式编辑器对话框。

（5）定义输出请求表达式为`{siso_0.OUTPUT}`。此表达式将输出X的状态。

STEP 03 求解单入单出系统

（1）单击Save按钮 ，保存模型为Spring_Transfer.mdl。

（2）单击工具栏中的Run按钮，进入Run面板。

（3）进入Simulation Parameter标签，将End time设置为5，其余使用默认设置。

（4）返回Main标签，单击“文件浏览”按钮。

（5）指定工作文件夹，将模型保存为Spring_Transfer.xml。

（6）单击Run按钮，求解模型。

3.线性系统方程方法

STEP 01 定义求解器变量

本例将f作为系统输入，x作为系统输出，因此只需定义线性系统的常系数矩阵。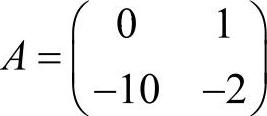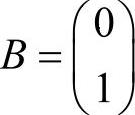，。这里使用求解器变量定义系统输入。

（1）启动MotionView，新建一个会话。

（2）从项目浏览树中右击Model，选择Add Control Entity→Solver Variable（或右击工具栏中的“求解器变量”按钮）。

（3）在弹出的Add Solver Variable对话框中，指定标题为f。

（4）使用默认的变量名。

（5）单击OK按钮。

（6）在求解器变量面板的Properties标签中，选择变量类型为Linear，并指定数值为10。

STEP 02 定义系统状态与输入矢量

（1）从项目浏览树中右击Model，选择Add Control Entity→Solver Array（或右击工具栏中的“求解器变量”按钮）。

（2）在弹出的Add Solver Array对话框中，指定标题为U。

（3）使用默认的变量名。

（4）在Solver Array面板的Properties标签中，将Array type设置为U，如图9-15所示。

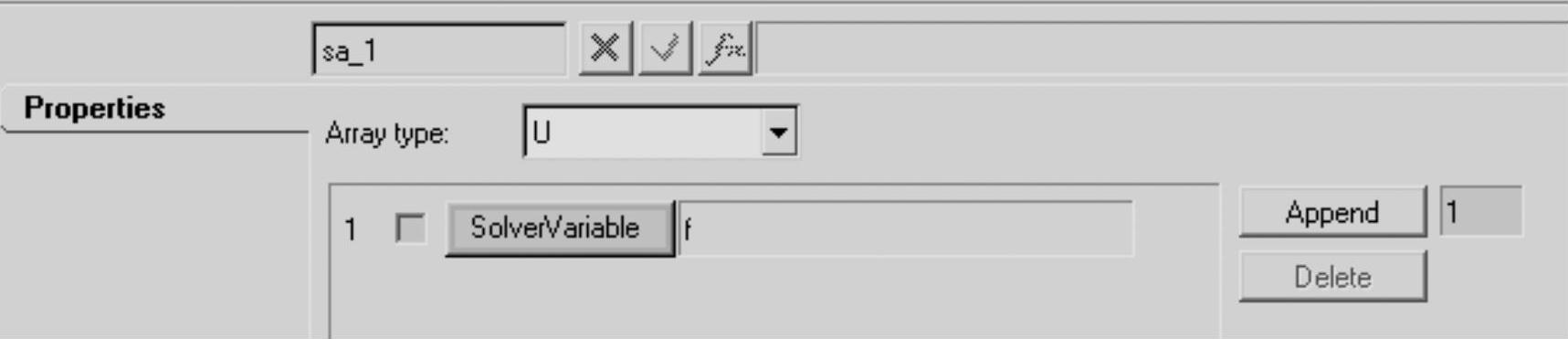
图9-15 Solver Array面板

（5）单击SolverVariable按钮，选择上步定义的求解器变量f。该矢量用于提供输入。

（6）新建一个标题为X的Solver Array。

（7）在Solver Array面板的Properties标签中，将Array type设置为X。该矢量用于定义系统状态。

STEP 03 定义线性系统常数矩阵

目前，MotionView不支持矩阵对象的建模，因此需要手动编辑求解器文件。本步首先将上述创建的模型导出，然后对其进行编辑。

（1）单击Export Solver Deck按钮。

（2）在弹出的Export Solver Deck对话框中单击“文件浏览”按钮，指定工作路径。

（3）将模型保存为Spring_Linear.xml。

（4）使用文本编辑器打开Spring_Linear.xml。

（5）在命令行＜/Model＞前定义常数矩阵A。

（6）定义常数矩阵B。

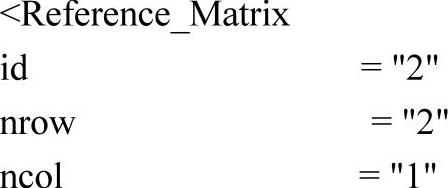
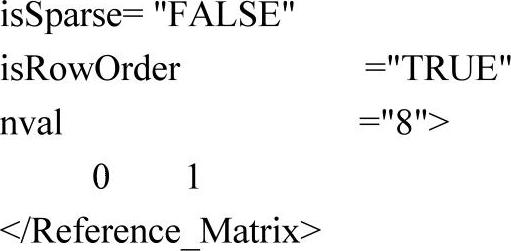
（7）定义状态方程。

（8）保存模型。

STEP 04 求解线性系统

（1）启动MotionSolve。

（2）找到上步保存的Spring_Linear.xml文件。

（3）单击Run按钮，求解模型。

STEP 05 查看结果

（1）启动HyperGraph。

（2）单击Data file栏的“文件浏览”按钮，载入Spring_Diff.abf文件，定义绘制曲线，如图9-16所示。

图9-16 Build plots面板（载入Spring_Diff.abf文件）

（3）单击工具栏中的Define plot按钮。

（4）将曲线名称修改为Spring_Diff，如图9-17所示。

（5）单击Build Plots按钮，进入Build Plots面板。

（6）单击Data file栏的“文件浏览”按钮，载入Spring_Transfer.abf文件，定义绘制曲线如图9-18所示。

（7）将曲线名称修改为Spring_Transfer。

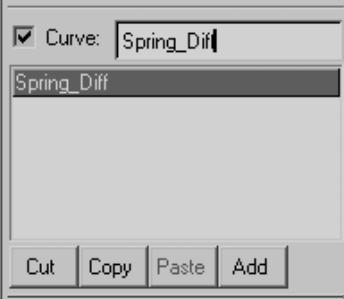
图9-17 Define plot面板

图9-18 Build plots面板（载入Spring_Transfer.abf文件）

（8）类似地，载入Spring_Linar.abf文件。绘制曲线，如图9-19所示。

图9-19 Build plots面板（载入Spring_Linar.abf文件）

（9）将曲线名称修改为Spring_Linear。

（10）此时图形区曲线如图9-20所示。可以看出3种方法获得的结果相同，即方块在重力作用下位移变化稳定于1m。读者可以试着创建弹簧阻尼-质量系统虚拟样机模型，求解并对比结果。

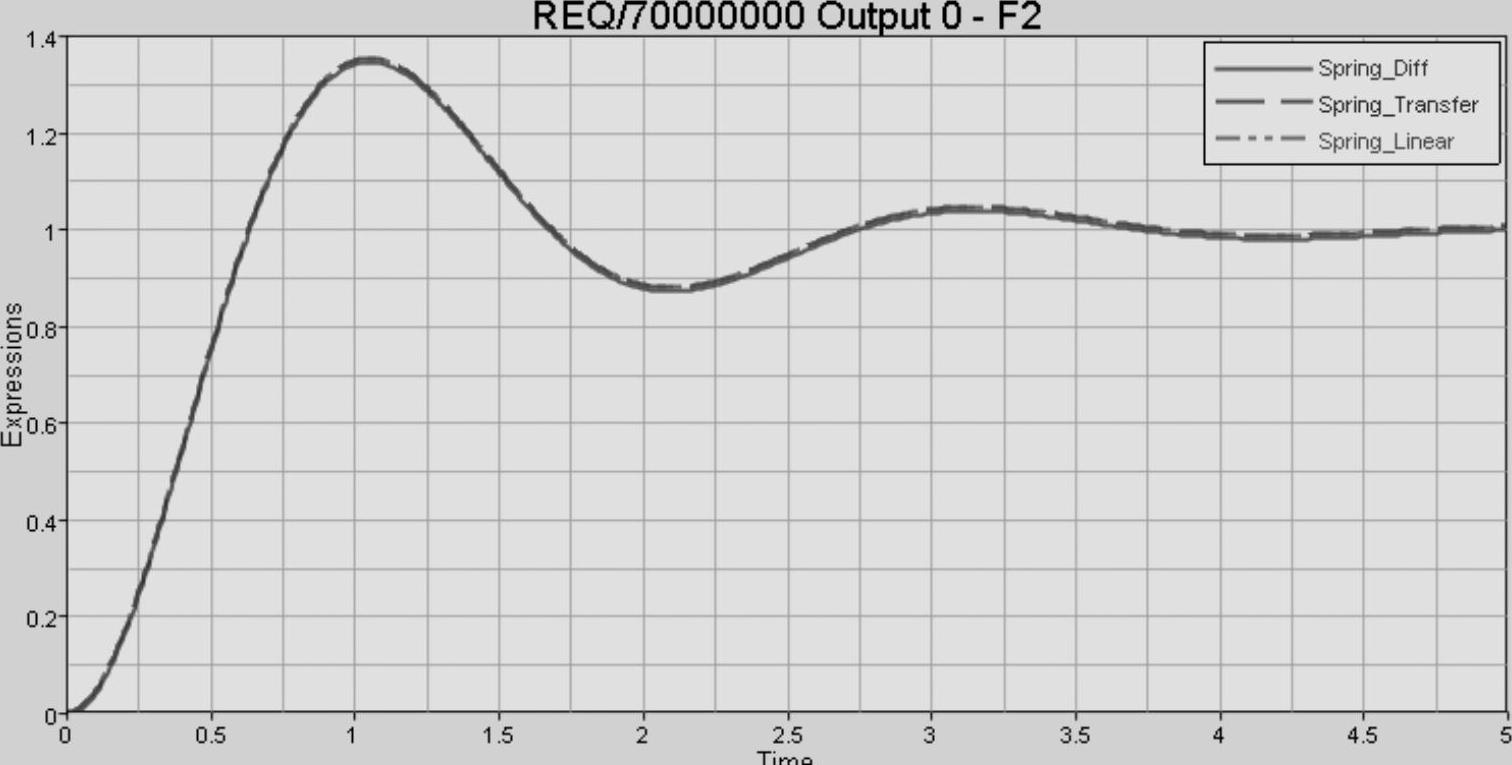
图9-20 曲线对比