进行ESL优化时，需为柔性体定义局部边界条件。在多体系统瞬态分析时，柔性体和刚性体由铰链连接，而在进行静态载荷等效时，这些铰链在基于静态响应结构优化中不再适用，也就是说柔性体将出现6个刚体模态。因此，在结构分析时需要去除模型中每个柔性体的6个刚体模态。这里去除的柔性体自由度精确为6个，如果约束了多于6个自由度，柔性体将被额外的约束限制，将增加ESL优化外循环的迭代次数并且可能无法获得最优的结果。

由于静态载荷等效时，每个柔性体在每次外循环的第0次内循环处于平衡位置。因此，可以固定任意6个自由度（通常固定一个节点）去除柔性体所有刚体模态进行等效静力分析。每个内循环的第0次迭代约束节点的反力为零，因而尽管柔性体6个自由度被限制，却没有额外的载荷加载的到柔性体上。然而随着内循环迭代的进行，模型中原始平衡被打破，从第1次循环开始，系统不再保持平衡。由此造成的不利结果是约束点处的反力不再是零，也就意味着有附加载荷作用在约束点。随着结构形状或尺寸的变化，这种不利影响可通过以下方法最小化。

去除柔性体6个刚体模态最常用的方法是固定一个节点的6个自由度。选择固定节点时，尽量选择不在高应力区域的节点。如果约束节点位于高应力区，将不容易获得最优结果。这里，推荐选择蛛网单元的独立节点或用于模拟铰链的刚性单元作为约束节点。实体单元模型，节点没有旋转刚度，如果模型中没有合适的刚性单元作为约束节点，那么最佳做法是通过固定一个节点的3个平动自由度（123）、第二个节点的两个平动自由度（23）和第三个节点的一个平动自由度（3）来去除柔性体的6个刚体模态。这3个节点选取时要保证其不在高应力区域，否则将达不到预期的效果。约束节点时，可使用SPC、SPC1或SPCADD卡片定义。

图8-7描述了一个包含两个铰接孔的实体单元模型约束方法。图8-8显示了两个时间步中的应力云图。

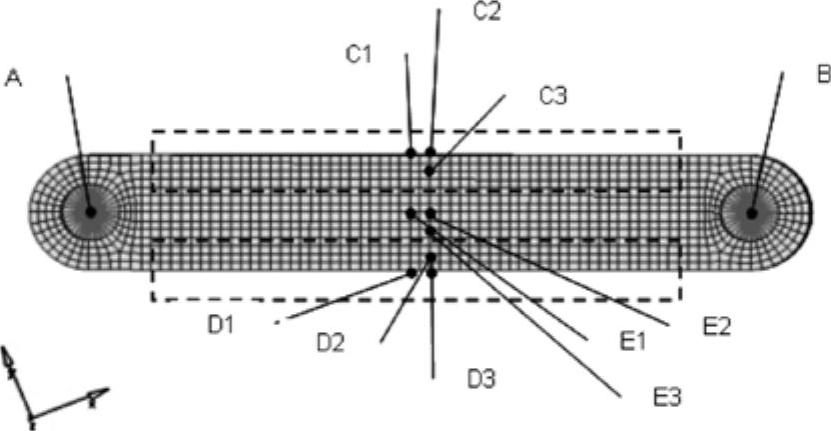
图8-7 实体单元约束定义

图8-8 两个时间步中的应力云图(www.daowen.com)

图8-7中的节点A与节点B是铰链连接点。该模型最佳的约束方式是固定节点A或节点B的6个自由度。其他方法可以是固定节点E1的3个平动自由度（123）、E2的两个平动自由度（23）、E3的一个平动自由度（3）。这3个节点位于相对低应力区。在该模型中，如果固定C1、C2、C3或者D1、D2、D3，优化迭代将不容易收敛。

定义了柔性体的局部边界条件，优化模型中的位移约束可用来限制柔性体的最大变形。接下来以旋转悬臂梁优化的示例（如图8-9所示）说明这一问题。模型定义时，可以固定悬臂梁的左端点（见图8-10a）或中间点（见图8-10b）来满足变形约束，只要这些节点不影响形状扰动向量或对形状扰动向量影响很小。如果优化问题需要约束梁左端点和右端点之间的相对位移，那么限制左端点的6个自由度将便于测量这一相对位移。类似地，如果优化问题需要约束梁左端点和中间点之间的相对位移，那么限制中间点的6个自由度将便于测量这一相对位移。这里不管限制左端点还是中间点，产生的梁应力是相同的。如果优化问题仅仅是约束柔性体应力或最小化、最大化柔性体应力，则建模时只需限制柔性体中一个合适的节点。

图8-9 旋转悬臂梁

图8-10 不同固定位置产生的梁柔性变形

a）左端固定 b）中间固定