本练习将学习以下内容：

● 通过创建数组集，定义模型的计算开始时间、时间中点、计算终止时间以及载荷大小。

● 在分析模型中调用数组集。

● 定义输入扭矩的载荷-时间关系。

在模型定义过程中，用户可能会接触到各种类型的数据及其组合，如字符串、整数、实数等。在MDL中，数组集（Dataset）是用户自定义的一系列数据的集合。创建完毕的数组集，可以在MotionView用户界面中进行查看、编辑、保存或删除。在MDL语言中，数组集由语句*DefineDataset（）-*EndDefine（）定义并由*DataSet（）调用。

STEP 01 定义一个数组

（1）打开文本编辑器，新建一个MDL。

（2）创建*DefineDataset（）和*EndDefine（）语句。为了完成数组的定义和初始化，还需要在这两条语句之间填入其他内容。

（3）在这一步的练习中，需要在数组中定义的数据包括计算开始时间、时间中点、计算终止时间和扭矩大小。

上述数据均为实数型数据，因此在数组语句中，需要使用*Real（）引导。每定义一个数据，需要新建一条*Real（）语句。当然，用户也可以根据需要，定义其他类型的数组数据，如整数型数据、字符串等。

完成定义的数组需要使用*Dataset（）语句进行实例化。*Dataset（）语句的基本格式如下：

*DataSet（ds_name，"ds_label"，ds_def，[optional arguments]）

其中，ds_name是数组变量名，ds_label是该数组标题，ds_def是已有数组的变量名。

（4）在工作文件夹下，保存该数组文件名为dataset.mdl。定义完成的MDL模型应如下所示：

STEP 02 在分析模型中调用数组文件

（1）在文本编辑器中打开5.5.3节中创建的analysis.mdl模型，在*DefineAnalysis（）语句前使用*Include（）调用数据集，调用方法如下：

*Include（"dataset.mdl"）

（2）选择合适的变量名和标题完成模型实例化。

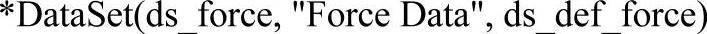
（3）通过*SetReal（）关键字，为数组成员指定初始值。*SetReal（）关键字语法如下所示：

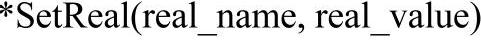
其中，real_name为变量名，real_value为变量值。

这里，实际的变量名应填写为Dataset def_var.real_name

如果对计算开始时间这一变量赋值，那么赋值语句应填写为

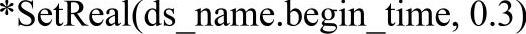
（4）使用类似的方法，完成数组中其他数据的赋值，并完成数组实例化，如下所示：

（5）在此前完成的模型中，可以查看到*SetForce（）已经按以下内容进行定义： *SetForce（force_1，'step（TIME，0.3，0，0.31，10）+step（TIME，0.31，0，0.32，-10）'，0，0）

（6）在文本编辑器中，将*SetForce（）内容改写为以下形式：(www.daowen.com)

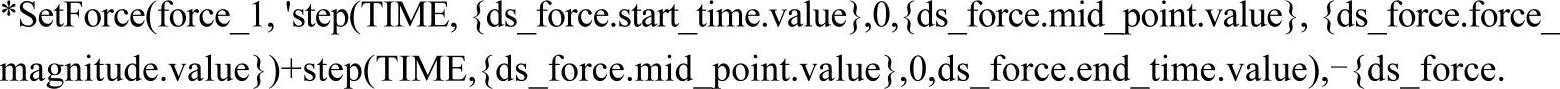
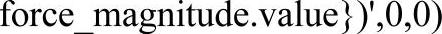
表达式中大括号“{}”中的内容将传递给MotionViewTemplex进行估值。

（7）在工作文件夹下，保存该数组文件名为analysis_new.mdl。定义完成的mdl文件应如下所示：

STEP 03 创建模型文件

（1）启动MotionView，并打开5.5.2节创建的（或目录chap05中的）triplependulum.mdl文件。

（2）在工具栏中单击System/Assembly按钮。

（3）在System/Assembly面板中激活Import/Export选项，单击“文件浏览”按钮，选择上述定义的分析模型文件analysis_new.mdl。

（4）单击Import按钮。

（5）在弹出的Specify entity details对话框中选择模型类型Analysis，如图5-39所示。

（6）单击OK按钮，载入分析模型。

图5-39 Specify entity details对话框

（7）在项目浏览树选择新载入的分析模型，在面板位置的Attachments标签中单击Joint按钮，并在图形区选择任一旋转副，如图5-40所示。

图5-40 System/Assembly面板（Attachments标签）

（8）在项目浏览树中右击Analysis 0，并选择Activate。

（9）打开Analysis 0下的Dataset Sets（1），单击Force Data。

（10）在主面板区域的Dataset面板中，修改Force Magmotide为20，如图5-41所示。

图5-41 Dataset面板

（11）选择File→Save as→model命令，将模型保存为new_dataset_triplependulum.mdl。

（12）在工具栏中单击Run按钮，进入Run面板。

（13）保存文件为new_dataset_triplependulum.xml并使用默认参数求解模型。

（14）求解结束后，单击Animate按钮查看三摆系统运动历程，单击Plot按钮查看指定的结果输出，如图5-42所示。

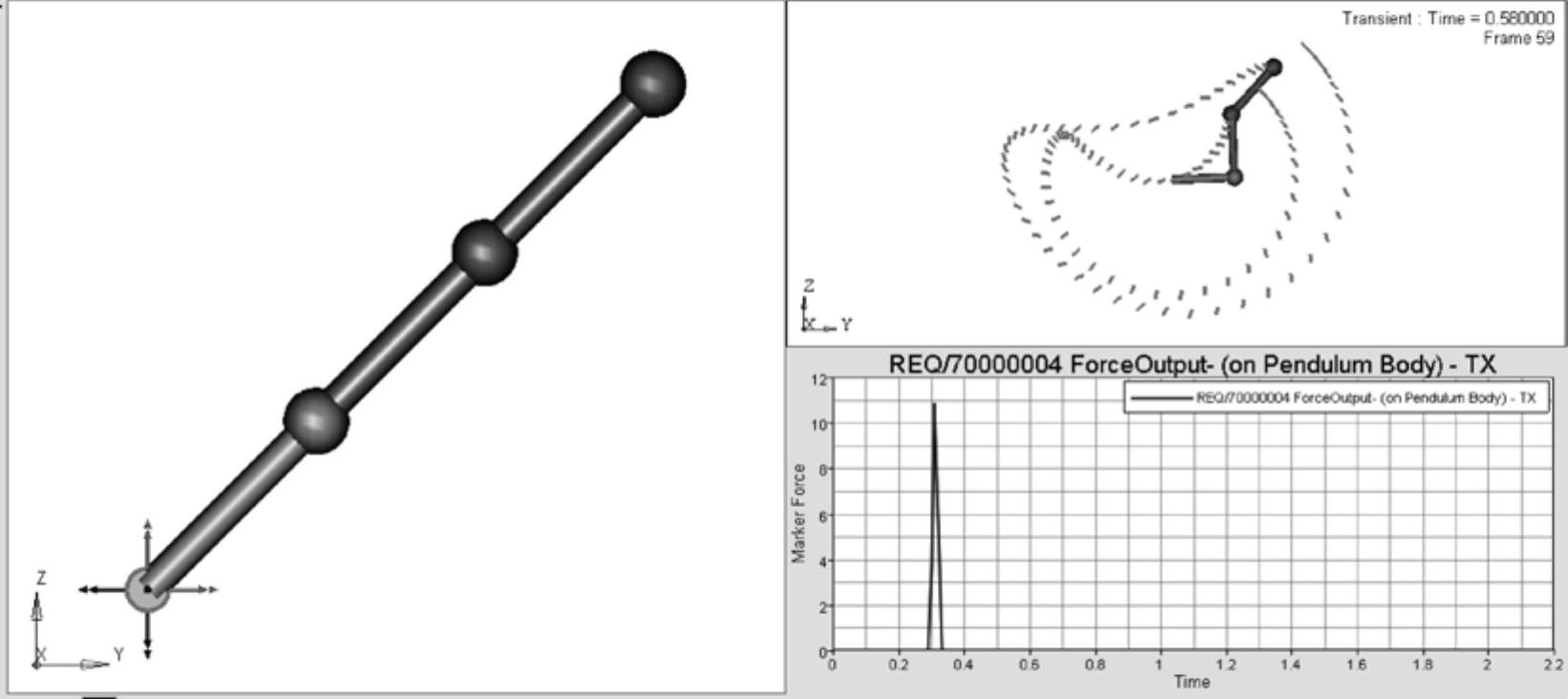
图5-42 三摆模型及分析结果